P7317 [COCI 2018/2019 #3] Praktični
题目描述
给定一个包含 $N$ 个结点和 $M$ 条边的无向图。每条边有一个小于 $10^9$ 的权值。
当一个环上的所有边的权值的异或和为 $0$,该环被称作好环。
可以对无向图进行若干次操作。每次操作包含下列步骤:
- 选定一个整数 $x$。
- 选定一个包含若干条边的非空集合。
- 给该集合中每条边都异或上 $x$。
请在尽可能少的操作次数之下使得无向图中的所有简单回路都是好环。请求出最少操作次数,并输出对应的操作参数。
输入格式
第一行输入正整数 $N,M$,分别表示结点和边的数量。
接下来的 $M$ 行中的第 $i$ 行,输入 $a_i,b_i,p_i$,分别表示第 $i$ 条边连接的结点和边的权值。保证图联通,且无重边。
输出格式
第一行输出 $K$,表示需要操作的最少次数。
接下来的 $K$ 行,每行输出若干个数,用空格分开:
- 第一个数为选定的数 $x$。
- 第二个数位 $B$,表示选定的边的数量。
- 接下来输出 $B$ 个数 $E_i$($1 \le E_i \le M$),表示选定的边的序号。这 $B$ 个数必须按照从小到大的顺序输出。
输出的所有数必须小于等于 $2 \times 10^9$。
说明/提示
#### 样例 1 解释
图的初始和结束状态(在初始状态的基础上给前三条边的权值异或上 $12$)分别如下方左图和右图所示:
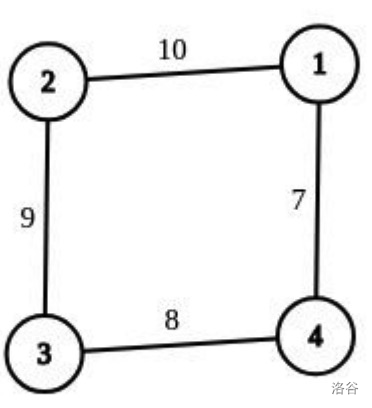
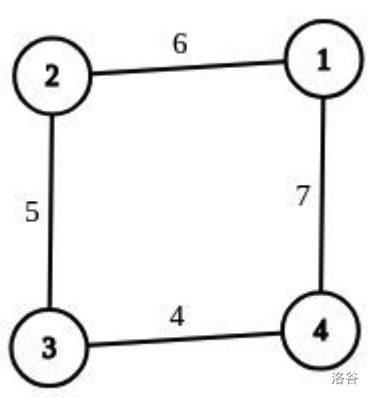
#### 样例 2 解释
该无向图无环,因此题意已经满足,不需要进行修改,因此最少操作次数为 $0$。
#### 数据规模与约定
对于 $20\%$ 的数据,$K=1$。
对于另外 $40\%$ 的数据,输入的所有数均小于等于 $10^6$。
对于 $100\%$ 的数据,$1 \le N,M \le 10^5$,$1 \le a_i,b_i \le N$,$a_i \neq b_i$,$0 \le p_i \le 10^9$。
#### 说明
**本题分值按 COCI 原题设置,满分 $130$。**
**题目译自 [COCI2018-2019](https://hsin.hr/coci/archive/2018_2019/) [CONTEST #3](https://hsin.hr/coci/archive/2018_2019/contest3_tasks.pdf) _T5 Praktični_。**