P7338 『MdOI R4』Color

小 M 同学有一张 $2$ 行 $n$ 列的方格纸，一开始所有格子都是白色的。 她决定对一些格子染色，具体地，每次她会选择两个**相邻的（四联通的，也就是有公共边的）白色**格子，其中一个染成红色，另一个染成蓝色。 她的目标是通过**任意次操作**让指定的一些格子变成红色，**对其他格子没有要求**。请你帮她判断一下，能否通过上述操作达成目标呢？

**本题包含多组数据。** 第一行有一个正整数 $T$ 表示数据组数。 接下来 $T$ 组数据，每组数据三行，包括： - 第一行，一个正整数 $n$ 表示方格纸列数。 - 第二行，一个 $01$ 串 $p_{1\ldots n}$，其中 $p_i=1$ 表示第 $1$ 行第 $i$ 列必须是红色，否则不作要求。 - 第三行，一个 $01$ 串 $q_{1\ldots n}$，其中 $q_i=1$ 表示第 $2$ 行第 $i$ 列必须是红色，否则不作要求。

$T$ 行，每行对应一组数据。 对于每组数据，如果可以做到输出 `RP`，否则输出 `++`。

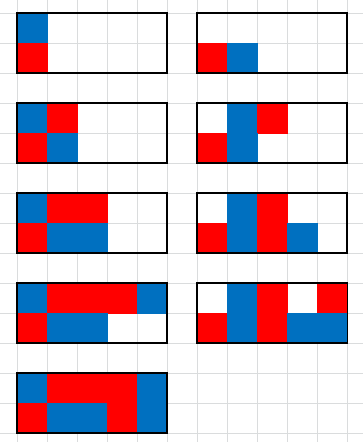
【样例解释】  上图中左侧为第一组测试数据的一种方案，右侧为第三组测试数据的一种方案，对于第二组测试数据，并没有满足要求的方案。 【数据规模与约定】 **本题采用捆绑测试** |子任务编号|$n\le$|特殊性质|$T\le$|分值| |:-|:-|:-|:-|:-| |$1$|$3$|无特殊限制|$10$|$10$| |$2$|$10$|无特殊限制|$10$|$20$| |$3$|无特殊限制|所有 $1$ 都在同一行|$10$|$1$| |$4$|无特殊限制|$1$ 不超过 $4$ 个|$10$|$13$| |$5$|$10^3$|无特殊限制|$10$|$25$| |$6$|无特殊限制|无特殊限制|$10$|$30$| |$7$|$16$|无特殊限制|$65536$|$1$| 对于所有数据，满足 $1\le n\le 10^5$，$\sum n\le 2^{20}$。