P7344 【DSOI 2021】积木
题目背景
"你听说过死亡游戏吗?就是将你关在一个暗无天日的房间里,给你一些琢磨不透的线索,倘若你不能解决问题,就给予你死亡的馈赠。
“嗯?慌什么,你现在仅仅是在这个不透风的房间里,我所要你回答的,也仅仅是个简单的问题而已。
“有意见吗?那好的,游戏开始。”
题目描述
“现在,你所拥有的是若干个棱长均为 $1$ 的正方体积木。而我,游戏的所有者,将会告诉你最终搭成的立体图形的主视图和左视图。你以为要你搭成这样的图形?别慌,游戏还远远没有这么简单。我将在这个图形中将主视图的其中几列给隐藏掉,如此一来,你就无法观察到他们的高度了。
“为了让这个游戏变得更有意思,我规定这些你无法观察到的数列的高度是任意的——这可以由你来决定。
“想必我亲爱的玩家,你小学时便知道,仅有主视图和左视图是无法确定一个图形的形状的,何况还有一部分被我隐藏了。因此,我们记 $k$ 为能够搭出我给出的图形的积木数,请你告诉我,最多有多少个整数 $k$ 能够满足我的要求呢? ”(即,请你**先自行决定好未知数列的取值**,**再根据这一取值来求出** $k$,你需要先决定高度使 $k$ 能取的值最多)
输入格式
**本题有多组数据。**\
第一行输入一个整数 $T$,表示数据组数。\
对于每一组数据:\
第一行输入两个整数 $n,m$,表示最终积木形状的长和宽。\
第二行包含 $n$ 个整数,第 $i$ 个整数 $a_i$ 表示主视图从左至右第 $i$ 列所看到的方块的高度。特别的,若 $a_i=-1$,则表示这一列的高度是任意的。\
第三行包含 $m$ 个整数,第 $i$ 个整数 $b_i$ 表示左视图从后至前第 $i$ 列所看到的方块的高度。保证不存在高度未知的列。
输出格式
对于每一组数据,输出一行一个整数,表示最多的能够满足要求的整数 $k$ 的数量。特别的,如果没有满足条件的整数 $k$,输出 $0$。
说明/提示
**【样例解释】**\
对于第一组数据:\
可行的 $k$ 值分别为:$6,7,8$。
对于每一个 $k$ 值,给出一种可能的构造如下(给出俯视图,数字表示该格的高度):
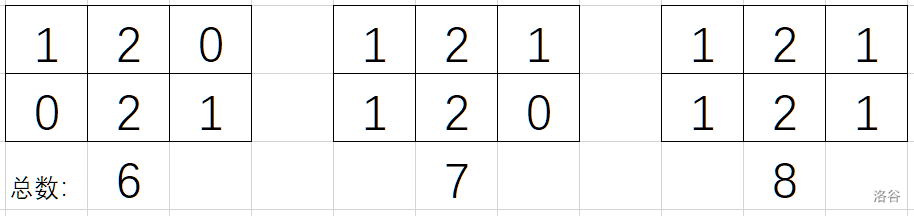\
对于第二组数据:\
当未知列的高度取 $2$ 时,满足要求的 $k$ 的数量最多,共有 $5$ 个,分别为:$4,5,6,7,8$。
**【数据范围和限制】**\
**本题采用捆绑测试。** 你必须通过 Subtask 中所有的测试点才能获得该 Subtask 的分数。
| Subtask | 分值 | $n,m,a_i,b_i \le$ | 特殊性质 |
| :-----: | :---: | :---------------: | :-----------------------------------: |
| 1 | 7pts | $3$ | 无 |
| 2 | 8pts | $10$ | 保证数列 $a$ 中 $-1$ 的数量不大于 $4$ |
| 3 | 8pts | $1000$ | 保证 $a_i \ne -1$ |
| 4 | 12pts | $2\times10^4$ | 保证 $a_i \ne -1$ |
| 5 | 7pts | $1000$ | 保证所有 $b_i$ 相等 |
| 6 | 8pts | $2\times10^4$ | 保证所有 $b_i$ 相等 |
| 7 | 15pts | $1000$ | 无 |
| 8 | 35pts | $2\times10^4$ | 无 |
对于 $100\%$ 的数据,满足 $1 \le n,m \le 2\times10^4,-1 \le a_i \le 2\times10^4,0 \le b_i \le 2\times10^4,0 \le T \le 100$。
本题读入数据量较大,请用**较快的读入方式**。