P7354 "PMOI-1" Cubic Knight

lhm has recently become obsessed with chess. He is most interested in the knight, so he created the following gameplay.

lhm has built a chessboard of size $n \times m$. You, as White, will fight against Black. Black has only one king, and **the king’s position will not move**. lhm has an unlimited number of knights. Now you need to find the minimum number of knights required to checkmate the Black king. The checkmate standard is defined as: **the Black king cannot move without being captured**. More formally: on an $n \times m$ board there is a king. You need to place as few knights as possible on the board such that for every position that the king can reach in **exactly one step** and is still inside the board, there exists at least one knight that can reach it in **exactly one step**. Piece movements: - The king can move one square each step in eight directions: up, down, left, right, up-left, up-right, down-left, down-right. - The knight moves the same as in standard chess: each move is an L-shape (i.e., the diagonal of a $2 \times 3$ rectangle; see the sample). **Note that there is no “blocked knight” rule: as long as it does not leave the board and follows the L-shape, there are no other restrictions.** lhm is not good at this, so he asks smart you to help him complete this task.

**This problem contains multiple test cases**. The first line contains an integer $T$, the number of test cases. For each test case, one line contains four integers $n, m, x, y$, representing the board size and the coordinates of the Black king.

Output $T$ lines in total. Each line contains one integer, the minimum number of knights needed.

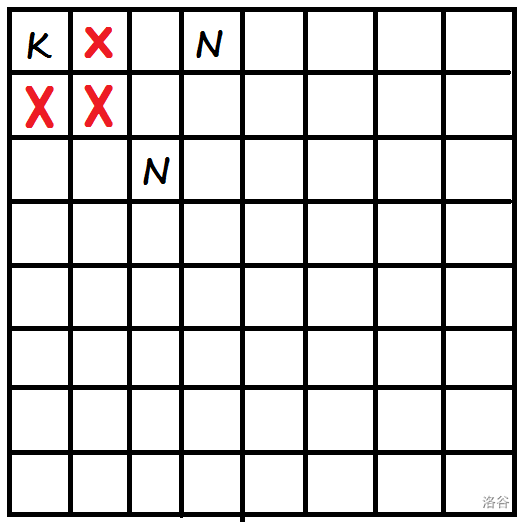
[Sample 1 Explanation]  On a board like the one above, $\text{K}$ represents the Black king, $\text{N}$ represents a White knight, and $\color{red}{\times}$ represents squares that a knight can reach (among them, the $\text{N}$ at $(3,3)$ blocks $(1,2)$ and $(2,1)$, and the $\text{N}$ at $(1,4)$ blocks $(2,2)$). As shown above, $\text{K}$ has already been completely trapped, so two knights are enough. It can be proven that two knights is the minimum. [Constraints] - For $30\%$ of the testdata, the king’s initial position is guaranteed to be on the outermost ring of the board. - For $100\%$ of the testdata, $1 \leq t \leq 10$, $1 \leq x,y \leq 10^9$, $8 \leq n,m \leq 10^9$. Translated by ChatGPT 5