P7367 [CTSC2002] 丹奇方块【征集 SPJ】

佳佳最近被一个叫做“丹奇方块”的游戏吸引住了，但是却因为游戏太难而迟迟无法通关。

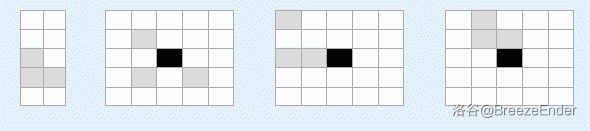
游戏在一个没有边界的棋盘上进行，中心 $(0,\,0)$ 处有一块黑色的障碍物，不远处坐标值为奇数的 $N$ 个不同的格子中各有一个灰色方块。 游戏的任务是把所有灰色方块全部粘起来组成一个给定的形状，如图一所示。该形状可以出现在棋盘上的任何位置，但不能旋转或者对称。图二描述了一个合法的初始状态，其中在坐标 $(-1,\,-1),\,(1,\,-1),\,(1,\,1)$ 处各有一个灰色方块。 游戏者每次可以用上（`U`）下（`D`）左（`L`）右（`R`）四种移动指令之一让所有的灰色方块同时往一个指定的方向移动一格。如果其中一个方块前方有障碍物，只有该方块便不能移动，其他方块仍然照常移动。例如，从图二的状态使用了指令 `LLUR` 后将形成图三所示的布局。一旦出现图三这样有两个或多个方块相邻的情况，这些相邻的方块会立刻粘在一起形成一块无法分离的整体，使得在今后的移动中，只要其中任意一个方块运动前方有障碍，即使其他方块并未被挡住，这个整体也无法移动。这样，在图三的状态使用指令 `URD` 后形成图四。由于图四中的灰色方块正好组成了该形状，游戏胜利结束。  这个游戏看起来简单，但方块数目多，目标形状又很复杂的时候游戏者往往需要很多步才能完成。佳佳希望找到一个不超过 $2000$ 步的解决方案，你能帮帮他吗？

第一行包含一个整数 $N$，即方块个数。 第二行包含 $N$ 个整数对 $x_i,\,y_i$ 其中第 $i$ 个整数对代表第 $i$ 个方块的初始位置。位置按照从上到下（即 $x$ 递增）从左到右（即 $y$ 递增）的顺序排列。 第三行包含 $N$ 个整数对 $P_{x_i},\,P_{y_i}$，代表目标形状中各小方块的相对位置。目标方块保证是一个连在一起的整体，且数据总是有解的。

第一行为需要的步数 $S$，第二行为所求移动序列。

#### 数据规模与约定 对于 $100\%$ 的数据，$3 \leq N \leq 20$，$-9 \leq x_i,\,y_i \leq 9$ 且 $x_i,\,y_i$ 为奇数，$1 \leq P_{x_i},\,P_{y_i} \leq N$。 #### 样例解释 参考输入格式，本题中 `D` 方向为 $x$ 轴正方向，`R` 方向为 $y$ 轴正方向。因此样例解释可参考题目描述第三段。