P7397 雨水收集系统（2021 CoE-I E）

Rain 市的环保部门为部分建筑的顶层安装了雨水收集装置，使得能够将雨水进行循环利用。雨水收集系统通过每栋建筑的顶层地面来收集雨水，利用特殊的管道将雨水集中引流到一个蓄水池中以待后续使用。环保部门计划根据降水量来估计蓄水池的容量大小以便进行设计制造。

为了简化问题的处理，将每栋建筑的顶层视为一个边与坐标轴平行的矩形，使用矩形的一条对角线顶点坐标来表示该矩形。每次降雨时，降雨云沿着特定的方向以一定的速度做匀速运动，降雨云所经过的区域均会有雨水降落。将降雨云抽象为一个凸多边形，给定初始时降雨云的位置以及移动方向和速率，确定在某段时间内雨水收集系统能够接受降雨的面积大小。

**输入包含多组测试数据**。 输入的第一行为一个整数 $T$，表示测试数据的组数，接下来共 $T$ 组数据，相邻两组测试数据之间有一个空行。每组测试数据的第一行为一个整数 $n$，表示建筑的数量。接下来 $n$ 行，每行四个整数，表示第 $i$ 栋建筑顶层所对应矩形的对角线顶点坐标。接下来一行是一个整数 $m$，表示降雨云对应凸多边形的顶点数目，接下来是 $m$ 个表示该凸多边形的顶点坐标（**不保证有序，即顶点可能不是按照顺时针或逆时针顺序给出，但给定的坐标点唯一地确定了表示降雨云的凸多边形**）：（$x_1$，$y_1$），（$x_2$，$y_2$），...，（$x_m$，$y_m$）。再接下来是起点 $s$（$x_s$，$y_s$）和终点 $e$（$x_e$，$y_e$）的坐标值，表示降雨云沿着从起点 $s$ 到终点 $e$ 的直线方向做平移运动。后续是一个整数 $v$，表示降雨云沿着直线方向的移动速率为 $v$ 单位距离/分钟，最后一行表示降雨的起始时间 $hh_{start}$ 时 $mm_{start}$ 分和结束时间 $hh_{end}$ 时 $mm_{end}$ 分，以 $24$ 小时计时法表示。

输出在指定时间内能够接受降雨的建筑顶层面积之和，精确到小数点后一位。如果你的输出和参考输出绝对误差在$10^{-1}$之内，均认为正确。

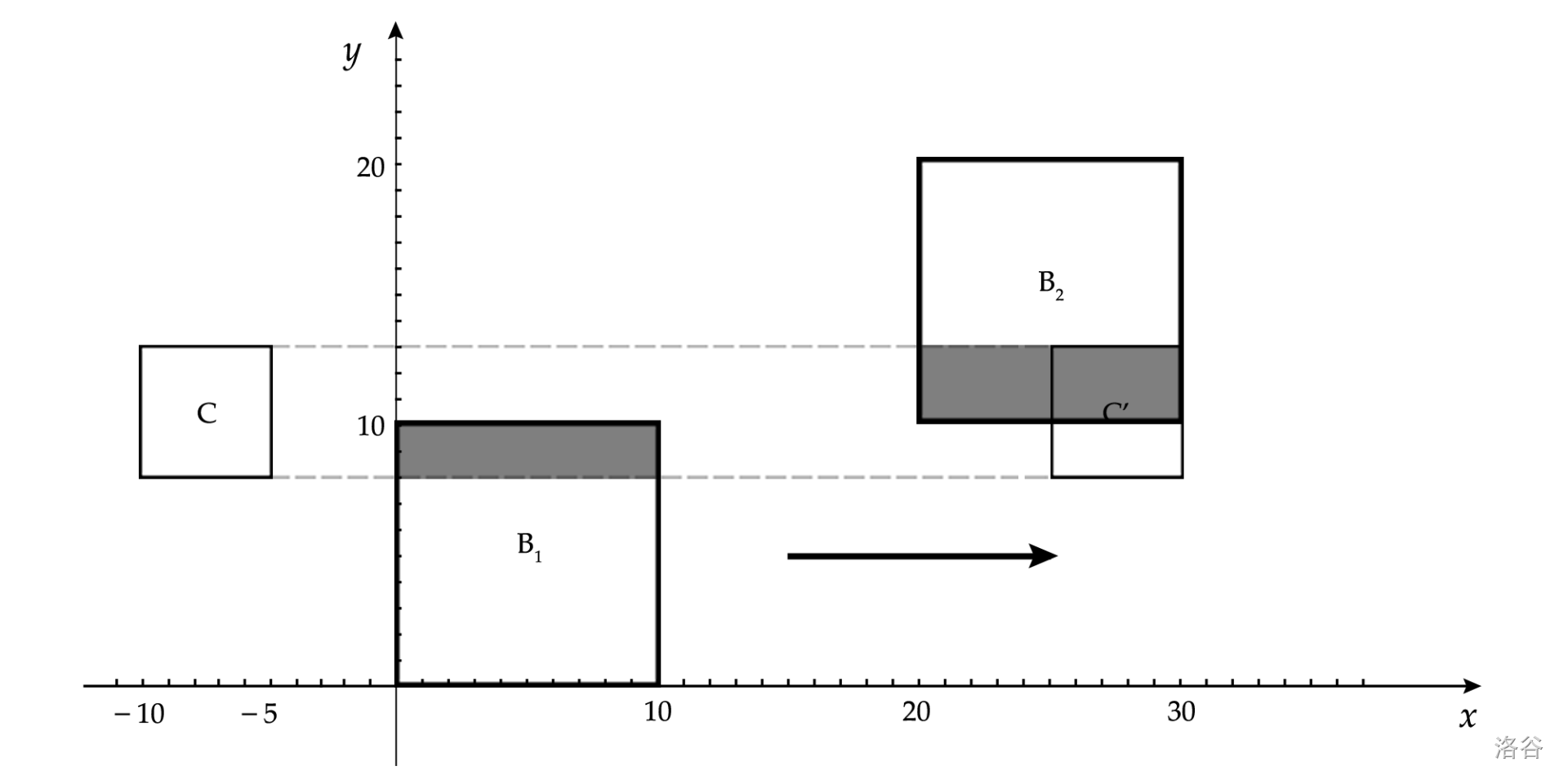
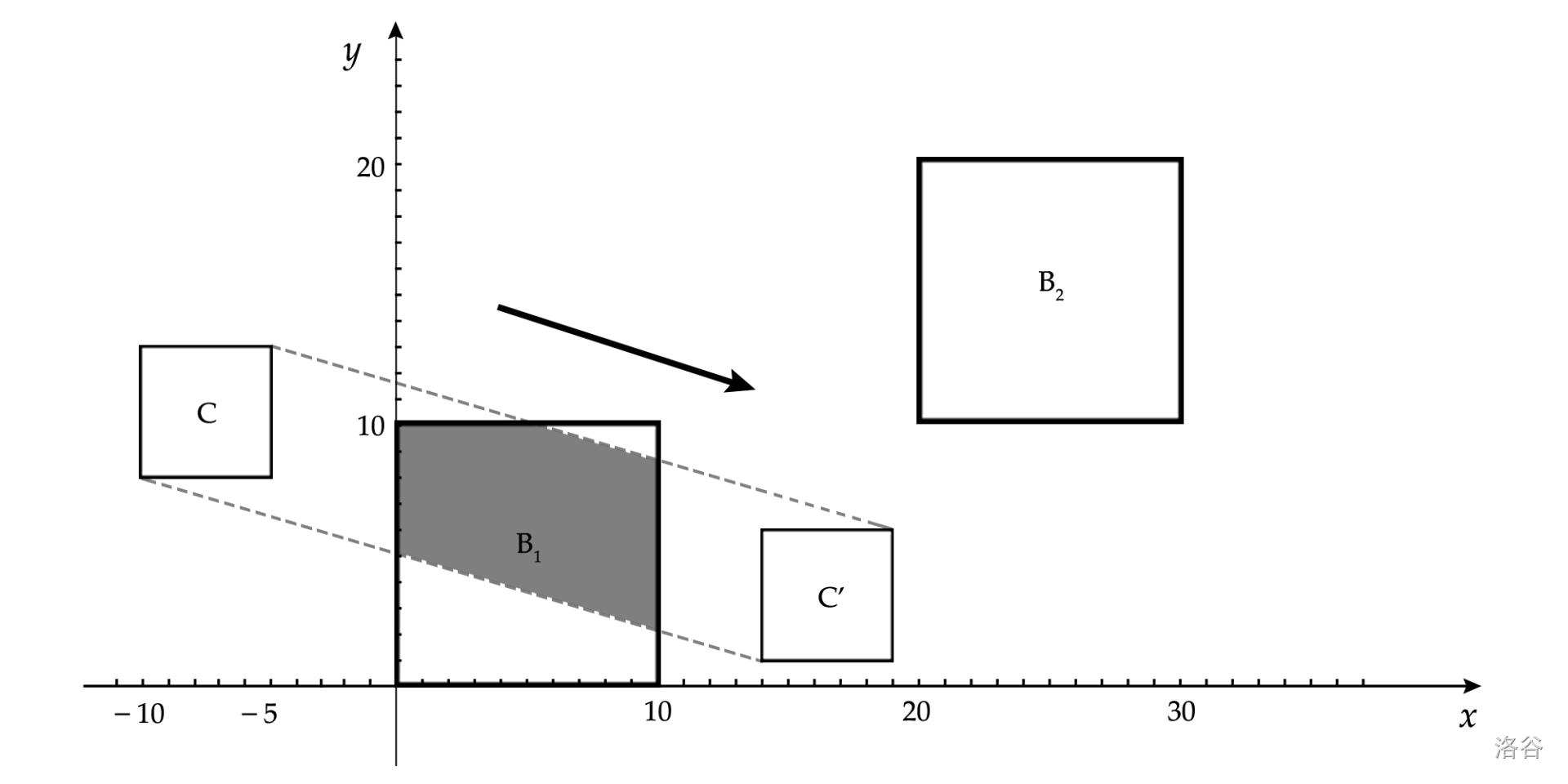
#### 样例说明  第一组测试数据，此组测试数据一共有 $2$ 栋建筑 $\operatorname{B_1}$ 和 $\operatorname{B_2}$，降雨云 $\operatorname{C}$ 为一个正方形（正方形的左下角位于坐标点（$-10$，$8$），边长为 $5$），降雨云沿着从起点（$15$，$0$）到终点（$25$，$0$）的方向匀速移动，移动速率为 $1$ 单位距离/分钟，降雨起始时间为 $15$ 时 $30$ 分，结束时间为 $16$ 时 $05$ 分，降雨时间为 $35$ 分钟，降雨云沿着箭头所示方向移动了 $35$ 单位距离。如上图所示，能够接受降雨的面积为阴影区域的面积，易知面积为 $50.0$。  第二组测试数据，降雨云的移动方向不同，从起点（$-5$，$8$）到终点（$19$，$1$）的方向匀速移动，降雨时间为 $60$ 分钟，沿着箭头所示方向的移动距离为 $60$ 单位距离，其他条件相同，能够接受降雨的面积为上图中的阴影区域，其面积为 $60.5$。注意，第二组测试数据的示意图中，为了示意的方便，所绘制的降雨云“最终位置”并不是其实际的最终位置。 ------------ #### 数据范围与约定 对于 $100\%$ 的数据，$1 \leq T \leq 10^3$，$1 \leq n \leq 50$，$3 \leq m \leq 100$，$0 \lt v \leq 100$。所有坐标值均为整数，位于闭区间 $[-10^5,10^5]$。 输入数据保证表示建筑顶层的矩形不会发生重叠。降雨的结束时间一定晚于起始时间。表示降雨云移动方向的起点 $s$ 和终点 $e$ 不同。