P7400 [COCI 2020/2021 #5] Magenta

给定一个包含 $n$ 个结点，$n-1$ 条边的连通图，其中结点编号分别为 $1,2,\cdots,n$。这 $n-1$ 条边被涂成了不同的颜色，其中包含蓝色、红色和洋红。 Paula 和 Marin 的棋子分别从结点 $a$ 和 $b$ 出发。两人轮流行走，Paula 先走。Paula 的棋子只能沿着蓝色或洋红的边行走，而 Marin 的棋子只能沿着红色或洋红的边行走。然而，任何时候都不能行走都对方棋子所在的位置。如果由一方的棋子无法行走，则另一方获胜。 如果 Paula 和 Marin 每次都使用最优的走法，求最终胜利的一方。如果游戏无法决出胜负，则为平局。

第一行输入整数 $n$，表示结点的数量。 第二行输入整数 $a,b$，表示 Paula 和 Marin 棋子的初始位置。 接下来的 $n-1$ 行，每行输入两个整数 $x,y$ 和一个字符串 $\text{color}$。如果 $\text{color}$ 为 $\texttt{plava}$，则表示连接 $x,y$ 的边的颜色为蓝色；如果为 $\texttt{crvena}$，则表示颜色为红色；如果为 $\texttt{magenta}$ 则为洋红。

如果 Paula 获胜，则输出 $\texttt{Paula}$。 如果 Marin 获胜，则输出 $\texttt{Marin}$。 如果游戏平局，则输出 $\texttt{Magenta}$。

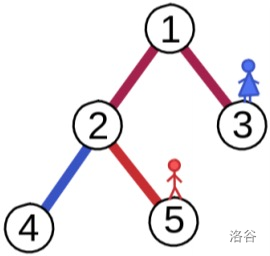
#### 样例 1 解释 Paula 的最优走法为前往结点 $2$，此时 Marin 无法行走。 #### 样例 2 解释 Paula 将前往结点 $1$，而 Marin 会前往结点 $2$。Paula 只能前往结点 $3$，此时 Marin 前往结点 $1$。这时 Paula 无法行走，Marin 获胜：  #### 数据规模与约定 **本题采用捆绑测试**。 |Subtask|分值|数据范围及约定| | :----------: | :----------: | :----------: | |$1$|$30$|$2 \le n \le 100$| |$2$|$30$|连通图中所有边的颜色都为洋红| |$3$|$50$|无| 对于 $100\%$ 的数据，$2 \le n \le 10^5$，$1 \le a,b \le n$，$a \neq b$，$1 \le x,y \le n$。 #### 说明 **本题分值按 COCI 原题设置，满分 $110$。** **题目译自 [COCI2020-2021](https://hsin.hr/coci/) [CONTEST #5](https://hsin.hr/coci/contest5_tasks.pdf) _T3 Magenta_。**