P7452 [THUSC 2017] 换桌
题目描述
班级聚会的时候,班主任为了方便管理,规定吃饭的时候同一个寝室的同学必须坐在一起;但是吃完饭后,到了娱乐时间,喜欢不同游戏的同学会聚到一起;在这个过程中就涉及到了座位分配的问题。
有 $n$ 张圆桌排成一排(从左到右依次编号为 $0$ 到 $n-1$),每张桌子有 $m$ 个座位(按照逆时针依次编号为 $0$ 到 $m-1$),在吃饭时每个座位上都有一个人;在吃完饭后的时候,每个人都需要选择一个新的座位(新座位可能和原来的座位是同一个),具体来说,第 $i$ 桌第 $j$ 个人的新座位只能在第 $L_{i,j}$ 桌到第 $R_{i,j}$ 桌中选,可以是这些桌中的任何一个座位。确定好新座位之后,大家开始移动,移动的体力消耗按照如下规则计算:
移动座位过程分为两步:
1. 从起始桌移动到目标桌**对应座位**,这个过程中的体力消耗为**两桌距离的两倍**,即从第 $i$ 桌移动到第 $j$ 桌对应座位的体力消耗为 $2\times |i-j|$;
1. 从目标桌的对应座位绕着桌子移动到目标座位,由于桌子是圆的,所以客人会选择**最近的方向**移动,体力消耗为**移动距离的一倍**,即从编号为 $x$ 的座位移动的编号为 $y$ 的座位的体力消耗为 $\min(|x-y|,m-|x-y|)$;
详情如下图:

现在,给定每个客人的限制(即每个人的新座位所在的区间),需要你设计一个方案,**使得所有客人消耗的体力和最小;本题中假设客人在移动的时候互不影响。**
输入格式
从标准输入读入数据。
第一行输入两个数 $n$ 和 $m$;
接下来输入 $n$ 行,每行 $m$ 个空格隔开的整数描述矩阵 $L$:其中,第 $i$ 行的第 $j$ 个数表示 $L_{i,j}$;
接下来输入 $n$ 行,每行 $m$ 个空格隔开的整数描述矩阵 $R$:其中,第 $i$ 行的第 $j$ 个数表示 $R_{i,j}$;
数据是随机生成的,生成数据的伪代码如下:
```cpp
for i
输出格式
输出到标准输出。
输出总体力消耗的最小值,如果没有合法的方案输出 `no solution`。
说明/提示
#### 样例解释
对于样例 $1$,
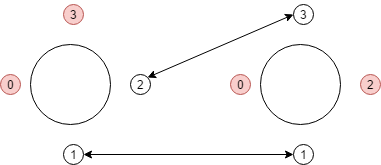
第 $0$ 桌的 $0$ 和 $3$ 号,以及第 $1$ 桌的 $0$ 号和 $2$ 号都被限制为只能坐在他们原来的桌子(可以不是原来的座位),其他人分别需要换到第 $1$ 桌和第 $0$ 桌;
可以发现,最优方案如上图,总体力消耗为 $10$。
对于样例 $2$,所有人都想坐到第 $0$ 桌,所以没有合法的方案。
对于全部数据:$1\le n\le 300$,$1\le m\le 10$,$0\le L_i\le R_i\le n-1$ 。
| 测试点 | $n\le$ |
| :----------: | :----------: |
| 1~2 | $2$ | |
| 3~8 | $40$ | |
| 9~14 | $100$ | |
| 15~20 | $300$ | |