P7498 磁控法则

>那只不过是别人的不幸。 诺顿进入了一个结构复杂的洞穴。在之前的勘察中，他已经得知了这个洞穴里有他梦寐以求的宝藏。 然而这个洞穴是如此的黑暗与复杂，以至于他探索了许久都没有找到宝藏的所在地。但宝藏强大的吸引力仍驱使着他继续搜寻。然而很快他就意识到了不对劲，因为那股吸引力不仅作用在他脑海中，也作用在他身体上——宝藏的防御机关正释放巨大的磁力试图驱逐外来者。 「果然，这就是它自带的保护机制吗？」诺顿笑了笑，拿出了一小块散发着奇特光芒的金属。 「不过，我也是有准备的。」

诺顿所在的洞穴可以看作是由 $n$ 个洞窟和 $n-1$ 条通道形成的树状结构，诺顿在石窟 $s$，宝藏在石窟 $t$。在宝藏所在的石窟里有一块拥有强大磁场的特殊的磁铁，诺顿身上也有一块小型的同样材质的磁铁。宝藏石窟里的磁铁**只有一个磁极**（N 或 S），并且**磁极不会发生变化**。诺顿身上的磁铁也**只有一个磁极**（N 或 S），但**每个时刻开始时会有 $p$ 的概率切换磁极**（N 变成 S，S 变成 N）。 每个时刻诺顿的移动方式由宝藏石窟磁铁的磁极和诺顿身上磁铁的磁极决定： 1. 两块磁铁磁极不同。此时两块磁铁会触发「吸引」效果。诺顿会因为磁铁间的吸引力移动到与 $s$ 相连的石窟中到 $t$ 距离 $-1$ 的石窟中（即**以 $t$ 为根时 $s$ 的父亲**）。 2. 两块磁铁磁极相同。此时两块磁铁会触发「弹射」效果。诺顿会因为磁铁间的排斥力**等概率**移动到与 $s$ 相连的石窟中到 $t$ 距离 $+1$ 的石窟（即**以 $t$ 为根时 $s$ 的任意一个儿子**）。如果没有满足的石窟，将触发「眩晕」效果，下个时刻诺顿将**不进行任何的移动，也不会进行任何的磁极切换**。 经过一段时间的勘察，诺顿已经知道了整个洞穴的结构以及磁极切换的概率 $p$。为了更好的寻找宝藏，他每次会向你提出询问，你需要回答他如果一开始诺顿在石窟 $x$，身上磁铁磁极为 $c_1$，宝藏在石窟 $y$，石窟内磁铁磁极为 $c_2$，期望在多少时刻后诺顿可以找到宝藏。

第一行三个整数 $n,q,p$，分别表示石窟数，询问数和磁极切换概率。其中磁极切换概率为在 $998244353$ 取模意义下的概率。 接下来 $n-1$ 行，每行两个正整数 $u,v$，表示石窟 $u$ 和石窟 $v$ 之间存在一条通道。保证最后结构为一棵树。 接下来 $q$ 行，每行**依次**有一个正整数 $x$，一个字符 $c_1$，一个正整数 $y$，一个字符 $c_2$，表示一个询问，各自意义如上。保证 $c_1,c_2$ 为 `N` 或 `S`。

$q$ 行，每行一个非负整数，表示询问答案对 $998244353$ 取模后的结果。

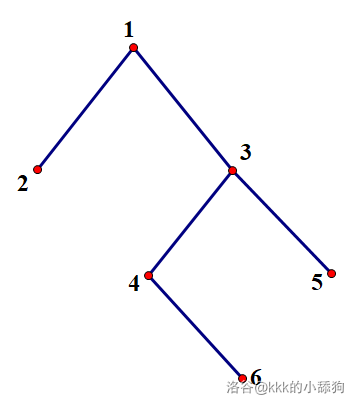
#### 样例一解释 每个时刻磁极切换概率为 $\dfrac{1}{2}$。 洞窟结构如下：  对于询问 $1$，诺顿在第 $1$ 个时刻有 $\dfrac{1}{2}$ 的概率移动到 $1$，有 $\dfrac{1}{2}$ 的概率触发「眩晕」进入第 $3$ 个时刻。在第 $3$ 个时刻同样有 $\dfrac{1}{2}$ 的概率移动到 $1$，有 $\dfrac{1}{2}$ 的概率触发「眩晕」进入第 $5$ 个时刻……期望结果为 $1\times\dfrac{1}{2}+3\times\left(\dfrac{1}{2}\right)^2+5\times\left(\dfrac{1}{2}\right)^3+\ldots=3$。 ------------ #### 数据范围 **本题采用捆绑测试**。 + Subtask 1 ( $10\%$ )：$n,q\leq15$。 + Subtask 2 ( $20\%$ )：$n\leq10^3$。 + Subtask 3 ( $25\%$ )：对于所有询问，保证 $y=1$。 + Subtask 4 ( $45\%$ )：无特殊限制。 对于所有数据，$2\leq n\leq5\times 10^5,1\leq q\leq5\times10^5,1\leq u,v,x,y\leq n,x\neq y,2\leq p\leq998244352$。 ------------ **本题读入量较大，请使用较快的读入方式。**