P7500 "HMOI R1" Metro Passenger Flow.

Metro passenger flow in a city is a very important indicator. It shows how many people are moving around in the city. Whether for commuting or tourism, it brings vitality to the city’s economy. During the pandemic, metro passenger flow in many places was very low, and some cities even suspended metro service. Now the situation is improving, and work and production are resuming in many places. Metro passenger flow is also an important reference for judging how much a city has resumed work and production, and how well the economy is recovering.

The metro system of Tiankong City consists of $M$ lines and has a total of $N$ stations. **Every station has lines stopping at it**. On each line, two adjacent stations can be viewed as connected by an undirected edge. Line $i$ has $k_i$ stations, and **these stations are all distinct**. These lines intersect at some stations, meaning that one station may have many lines stopping at it. Now, there are $P$ passengers. Passenger $j$ wants to travel from station $s_j$ to station $t_j$, and it is **guaranteed that these two stations are different**. If the two stations are not on the same line, the passenger will transfer several times. As a technical staff member of the Tiankong Metro, you need to compute the passenger flow contributed by these passengers. ------------- Note that the method used to compute passenger flow here is different from real-world applications. Passenger flow $=$ entry flow $+$ transfer flow. The entry flow is the number of passengers; the transfer flow is the number of transfers made by passengers. There may be multiple paths between the start and the destination; in that case, the metro passenger flow is independent of **which** path the passenger chooses. When calculating, we only consider paths with the **minimum number of transfers**. --------- Notes: - Suppose the minimum number of transfers from $s$ to $t$ is $\rm trans$. Then the passenger needs to take $\rm trans + 1$ lines, contributing $\rm trans + 1$ passenger flow. - When the passenger cannot reach the destination from the start (i.e., there is no path between $s$ and $t$), they will take a bus instead, and the passenger flow is counted as $0$.

The first line contains three integers $N, M, P$. The next $M$ lines each describe one metro line: The first integer in each line is $k_i\ (2 \le k_i \le N)$, the number of stations on this line; Then follow $k_i$ integers $q\ (1 \le q \le N)$, the station indices that this line passes through in order. The next $P$ lines each contain two integers $s_j, t_j\ (1 \le s_j, t_j \le N;\ s_j \neq t_j)$, describing the start and end stations of one passenger’s trip.

Output one integer in a single line, representing the passenger flow contributed by these passengers.

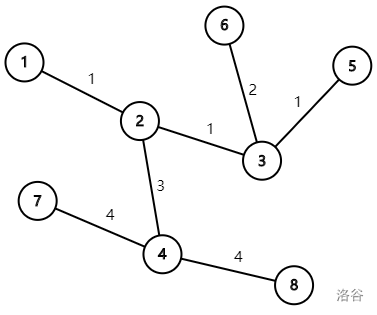
Sample explanation: - By default, passengers will choose a path with the minimum number of transfers. - The number on an edge indicates the index of the metro line it belongs to. Sample 1 is shown in the figure:  Passenger $1$ will take Line $1$ from $1$ to $3$, then take Line $2$ from $3$ to $6$; Passenger $2$ will take Line $3$ from $4$ to $2$, then take Line $1$ from $2$ to $3$; Passenger $3$ will take Line $4$ from $4$ to $8$; Passenger $4$ will take Line $2$ from $6$ to $3$, take Line $1$ from $3$ to $2$, then take Line $3$ from $2$ to $4$, and finally take Line $4$ from $4$ to $7$. Thus, the four passengers contribute passenger flow of $2, 2, 1, 4$ respectively, and the answer is $9$. 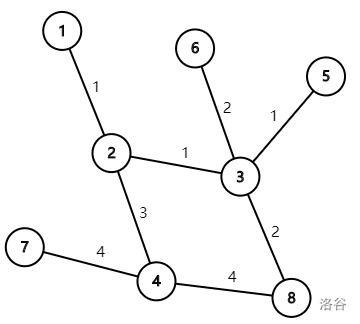Sample 2 is shown in the figure:  Compared with Sample 1, Passenger $2$ can choose another route: take Line $4$ from $4$ to $8$, then take Line $2$ from $8$ to $3$, which also involves one transfer; Passenger $4$ can choose another route with fewer transfers: take Line $4$ from $7$ to $8$, then take Line $2$ from $8$ to $6$, with only one transfer. The total passenger flow is $2 + 2 + 1 + 2 = 7$. 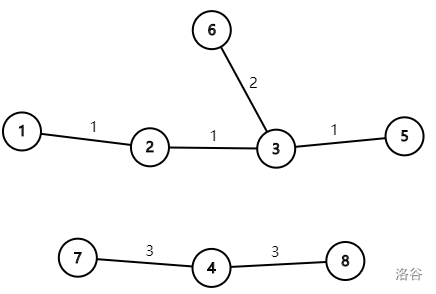Sample 3 is shown in the figure:  Compared with Sample 1, the travel paths of passengers $2$ and $4$ are not connected, so they are not counted in the passenger flow. The total passenger flow is $2 + 0 + 1 + 0 = 3$. ------------ Let the number of lines stopping at station $i$ be $\mathrm{siz}_i$. For all testdata: - $2 \le N \le 10^5$; - $1 \le M \le 1000$; - $1 \le P \le 100$; - $1 \le \mathrm{siz}_i \le 50$. -------- **This problem uses bundled tests.** | No. | Constraints | Score | | ---- | ------------------------ | ----- | | $1$ | $N, P \le 5;\ M \le 3$ | $10$ | | $2$ | $k_i = 2$ | $20$ | | $3$ | $N, M \le 50;\ P \le 10$ | $20$ | | $4$ | $M \le 500;\ P \le 10$ | $20$ | | $5$ | No further constraints | $30$ | ------------ Due to the large input size, do not use `cin` with stream synchronization enabled. You can disable synchronization for `cin` by using `std::ios::sync_with_stdio(false)`. You may also use the following fast input template, which supports reading non-negative integers within the `int` range. ```cpp int readInt() { int ret = 0; char o; while (!isdigit(o = getchar())); do ret = ret * 10 + (o ^ 48); while (isdigit(o = getchar())); return ret; } ``` ---------- - Idea: Nanqiao Bus Station (Nánqiáo qìchēzhàn). - Solution: Nanqiao Bus Station (Nánqiáo qìchēzhàn). - Code: Nanqiao Bus Station (Nánqiáo qìchēzhàn). - Data: Nanqiao Bus Station (Nánqiáo qìchēzhàn). Translated by ChatGPT 5