P7553 [COCI 2020/2021 #6] Geometrija
题目描述
平面内有不共线的 $n$ 个点。如果两条线段 $\overline{AB}$ 和 $\overline{CD}$ 有异于 $A, B, C, D$ 的公共点,则称他们「相交」。
记 $S$ 为 $n$ 个点两两相连得到的线段的集合。求不与 $S$ 中任意其他线段相交的线段数量。
输入格式
第一行一个整数 $n$。
接下来 $n$ 行,每行两个整数 $x_i, y_i$,表示第 $i$ 个点的坐标。
输出格式
一行一个整数,表示满足要求的线段的数量。
说明/提示
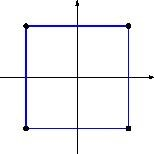
#### 样例 1 解释
符合要求的线段如图所示:
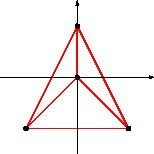
#### 样例 2 解释
符合要求的线段如图所示:
------------
#### 数据规模与约定
**本题采用捆绑测试**。
| Subtask | 分值 | 数据规模与约定 |
| :----------: | :----------: | :----------: |
| $1$ | $20$ | $3 \le n \le 40$ |
| $2$ | $30$ | $3 \le n \le 200$ |
| $3$ | $60$ | 无附加约定 |
对于 $100\%$ 的数据,$3 \le n \le 10^3$,$-10^9 \le x_i, y_i \le 10^9$。
------------
#### 说明
**本题分值按 COCI 原题设置,满分 $110$**。
**题目译自 [COCI2020-2021](https://hsin.hr/coci/archive/2020_2021/) [CONTEST #6](https://hsin.hr/coci/archive/2020_2021/contest6_tasks.pdf) _T4 Geometrija_**。