黑白棋（2021 CoE-II B）

$\text{Alice}$ 和 $\text{Bob}$ 正在玩一种称为“黑白棋”的游戏。该游戏的规则如下： - 游戏在直角坐标系中进行。 - $\text{Alice}$ 执黑棋，$\text{Bob}$ 执白棋。 - 初始时，在直角坐标系中任选 $n$ 条与 $X$ 轴平行的直线，直线在 $Y$ 轴上的截距均为整数，且互不相同。$\text{Alice}$ 在每条直线上都会放置一枚黑棋，$\text{Bob}$ 在每条直线上都会放置一枚白棋，棋子位置的 $X$ 坐标值均为整数。在同一条直线上的两枚棋子位置不会相同。 - $\text{Alice}$ 和 $\text{Bob}$ 轮流走棋，$\text{Alice}$ 总是先走棋。每名玩家在走棋时，先选择一条直线，然后沿着直线移动该条直线上己方颜色的棋子。 - 每个玩家可以将自己的棋子向着靠近对方棋子的方向一次性移动若干整数单位距离，称之为**前进**。每个玩家也可以向着远离对方棋子的方向一次性移动若干整数单位距离，称之为**后退**。只要在前进时不跨过对方的棋子，也不使黑棋和白棋的位置发生重叠，前进的最远距离不限，但是前进的距离至少为 $1$，如果无法满足前述条件，则玩家不能执行前进操作。为了避免玩家反复后退导致游戏无法结束，在一局游戏中，某个玩家执行后退操作的总次数不能超过 $k$ 次。与此同时，为了防止游戏区域太大以致在显示游戏状态上造成不便，每次后退的距离至少为 $1$，但不能超过 $d$。如果无法满足前述条件，玩家不能执行后退操作。 - 玩家在轮到自己走棋时，如果能够执行操作就必须执行一次操作，此操作可以是前进操作，也可以是后退操作（如果未超出后退次数的限制）。 - 如果某个玩家无法执行任何操作来移动自己的棋子，将输掉游戏，游戏结束。 给定游戏的初始状态，假设 $\text{Alice}$ 和 $\text{Bob}$ 在游戏时均采用最佳策略，试确定 $\text{Alice}$ 能否获胜。

**输入包含多组测试数据。** 输入第一行包含一个整数 $T$，表示测试数据的组数。接着是一个空行。接下来是 $T$ 组表示游戏初始状态的数据。 每组数据的第一行包含三个整数 $n$，$k$，$d$，表示直线的数量，允许后退的总次数，每次后退的最大距离。接下来是 $n$ 行数据，每行包含三个整数 $y_i$，$b_i$，$w_i$，分别表示第 $i$ 条直线的 $Y$ 轴截距以及在该条直线上的黑棋的 $X$ 坐标值和白棋的 $X$ 坐标值（$b_i \ne w_i$）。 每两组测试数据之间有一个空行。

如果 $\text{Alice}$ 能够获胜，输出 `Yes`，否则输出 `No`。

2

2 0 10
3 4 8
7 7 5

3 5 15
-3 -9 -19
-7 10 21
12 12 16

Yes
No

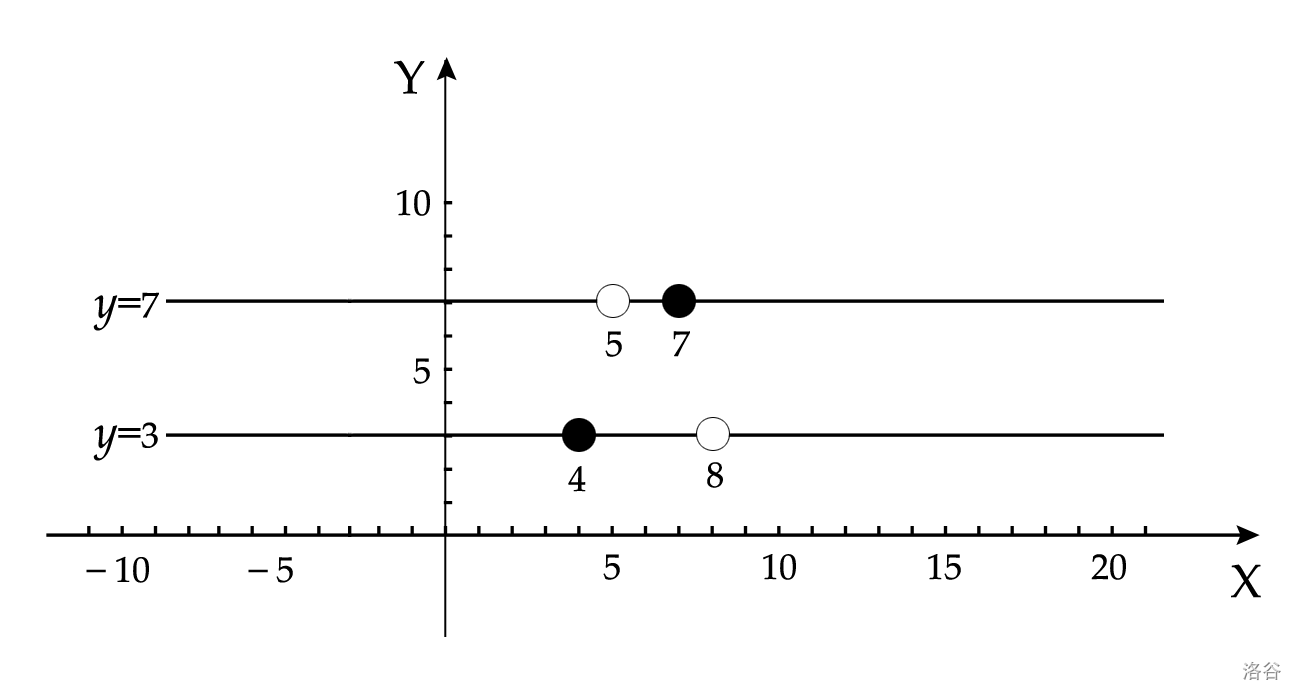
**样例说明** 下图对应输入 \#1 的第一组数据，如果 $\text{Alice}$ 采用最优策略，无论 $\text{Bob}$ 如何走棋，$\text{Alice}$ 都能够获胜。  以下是 $\text{Alice}$ 的必胜策略。首先，$\text{Alice}$ 选择将 $y=3$ 的直线上的黑棋从 `4` 移动到 `6`，使得两条直线上黑棋和白棋之间的间距均为 $2$，由于 $k$ 为 $0$，相当于不允许执行后退操作，如果 $\text{Bob}$ 选择移动 $y=3$ 直线上的白棋，将使得该直线上的两颗棋子相邻，后续无法再移动。同样的，如果 $\text{Bob}$ 选择移动 $y=7$ 直线上的白棋，也将使得该直线上的两颗棋子相邻，后续无法再移动。因此无论 $\text{Bob}$ 如何操作，总会使得一条直线上的两颗棋子相邻，无法再继续移动，而另外一条直线上的棋子间距为 $2$，还可以再移动一次，$\text{Alice}$ 将剩下可以移动的黑棋再移动一步后，后续 $\text{Bob}$ 无法移动白棋，因此 $\text{Alice}$ 会获胜。 对于输入 \#1 的第二组数据，无论 $\text{Alice}$ 如何走棋，$\text{Bob}$ 总能够获胜。 ------------ **数据范围** 对于 $100\%$ 的数据，$1 \le T \le 100$，$1 \le n \le 100$，$0 \le k \le 100$，$1 \le d \le 20$，$-100 \le y_i \le 100$，$-10^3 \le b_i \le 10^3$，$-10^3 \le w_i \le 10^3$。