P7591 狩猎（2021 CoE-II D）

母狮 $\text{Dina}$ 的领地里有固定的 $n$ 个狩猎点，第 $i$ 个狩猎点有 $p_i$ 的概率可以捕捉到猎物，$\text{Dina}$ 的巢穴和 $n$ 个狩猎点相互之间存在若干条直接连接的双向道路。 每天早晨，$\text{Dina}$ 从她的巢穴出发，随机选择一个与巢穴相邻的狩猎点 $u$ 进行一次捕猎，如果她未捕捉到猎物，她会随机选择一个与当前狩猎点 $u$ 相邻的其他狩猎点 $v$ 继续进行一次捕猎，如果在狩猎点 $v$ 仍未捕捉到猎物，$\text{Dina}$ 会按照前述过程继续捕猎。如果在某个狩猎点捕捉到了猎物，$\text{Dina}$ 会立即返回巢穴，结束捕猎。若当前狩猎点 $u$ 与巢穴相邻，而与其他狩猎点不相邻，$\text{Dina}$ 也会选择立即返回巢穴，然后从与巢穴相邻的狩猎点中，随机选择一个狩猎点继续上述捕猎过程。$\text{Dina}$ 在每个狩猎点只进行一次捕猎，然后离开，但后续可能还会回到该狩猎点再次进行捕猎。在本题环境下，如果地点 $u$ 和地点 $v$ 之间有一条直接连接的双向道路，称地点 $u$ 和地点 $v$ **相邻**，否则称地点 $u$ 和地点 $v$ **不相邻**。 令巢穴的编号为 $0$，$n$ 个狩猎点的编号从 $1$ 到 $n$，$\text{Dina}$ 从编号为 $u$ 的地点到达另外一个编号为 $v$ 的地点需要消耗 $h_{u,v}$ 体力和 $t_{u,v}$ 时间。在第 $i$ 个狩猎点每进行一次捕猎，$\text{Dina}$ 会消耗 $h_i$ 体力和 $t_i$ 时间。每当 $\text{Dina}$ 到达某个狩猎点并进行一次捕猎后，她会评估自己的体力消耗和时间花费，如果体力消耗已经达到（或超过）限值 $H$，她就选择立即返回巢穴结束捕猎。如果时间花费已经达到（或超过）限值 $T$，她也会选择立即返回巢穴结束捕猎。$\text{Dina}$ 只有在到达狩猎点并进行一次捕猎后才进行评估，在任何其他时刻均不会进行评估。如果当前位于巢穴，她会在到达巢穴时就进行评估，因为巢穴并无猎物可供捕捉。 需要注意，$\text{Dina}$ 在沿着两个地点间的双向道路移动的过程中并不会评估，因此可能会出现以下情形：到达某个狩猎点且尚未进行捕猎时，$\text{Dina}$ 已消耗的体力或者已花费的时间已经超过限值。在这种情形下，$\text{Dina}$ 仍然会进行一次捕猎，之后再进行评估。 当 $\text{Dina}$ 因为捕猎成功、体力消耗或时间花费达到（或超过）相应限值、当前狩猎点与其他狩猎点不相邻而返回巢穴时，她总会选择一条具有最少时间花费的路径。如果存在多条具有最少时间花费的路径返回巢穴，她会选择其中体力消耗最少的路径。$\text{Dina}$ 在返回巢穴的过程中不会进行捕猎。 将 $\text{Dina}$ 从巢穴出发，因满足以下三个条件之一： - 捕猎成功 - 体力消耗达到（或超过）限值 $H$ - 时间花费达到（或超过）限值 $T$ 返回到达巢穴并结束捕猎的过程称为一次狩猎。给出巢穴和狩猎点之间的道路、每条道路所需要消耗的体力和花费的时间、每个狩猎点进行一次捕猎能够捕获猎物的概率以及所需消耗的体力、花费的时间，试确定 $\text{Dina}$ 完成一次狩猎所消耗体力和花费时间的平均值。

输入的第一行包含一个整数 $n$，表示狩猎点的数量。 接下来 $n$ 行，每行包含三个数值：整数 $h_i$，整数 $t_i$，实数 $p_i$，分别表示在第 $i$ 个狩猎点进行一次捕猎所消耗的体力、花费的时间、能够捕获猎物的概率。 接下来是一个整数 $m$，表示连接各个地点的双向道路的数量。接着 $m$ 行，每行包含四个整数 $u$，$v$，$h_{u,v}$，$t_{u,v}$，表示从编号为 $u$（$0 \le i \le n$）的地点到另外一个编号为 $v$（$0 \le i \le n$，$u \ne v$）的地点之间存在一条直接连通的道路，需要消耗 $h_{u,v}$ 体力和花费 $t_{u,v}$ 时间。由于是双向道路，从地点 $u$ 到达地点 $v$ 与从地点 $v$ 到达地点 $u$ 所消耗体力和花费时间相同。 最后是两个整数 $H$ 和 $T$，表示体力和时间的限值。

输出一行，包含两个实数，精确到小数点后一位，分别表示 $\text{Dina}$ 完成一次狩猎所消耗体力和花费时间的平均值。如果你的输出和参考输出绝对误差小于$10^{-1}$，均认为正确。

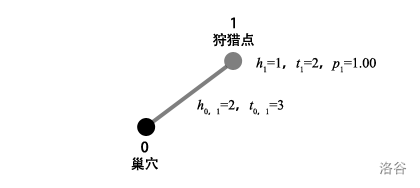
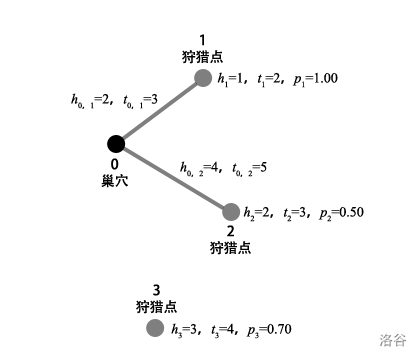
**子任务测试采用捆绑方式计分。** **样例说明** 输入 #1  该输入只包含一个狩猎点，从巢穴到狩猎点 $1$ 之间的道路需要消耗 $2$ 体力和 $3$ 时间，体力的限值为 $10$，时间的限值为 $20$，在狩猎点 $1$ 进行一次捕猎需要消耗 $1$ 体力和 $2$ 时间，在狩猎点 $1$ 捕获猎物的概率为 $1.00$，即一定会捕捉到猎物。容易知道，进行一次狩猎所消耗的体力和花费时间的平均值分别为 $5.0=(2+1+2) \times 100\%$ 和 $8.0=(3+2+3) \times 100\%$。 输入 #2  相较于第一组输入，新增了两个狩猎点，但只有狩猎点 $1$ 和狩猎点 $2$ 与巢穴有直接道路相连。三个狩猎点之间无直接道路相连，但狩猎点 $1$ 可以间接通过巢穴与狩猎点 $2$ 连通。从巢穴到狩猎点 $2$ 的道路需要消耗 $4$ 体力和 $5$ 时间，在狩猎点 $2$ 进行一次捕猎需要消耗 $2$ 体力和 $3$ 时间。在狩猎点 $1$ 捕获猎物的概率为 $1.00$，即一定会捕捉到猎物，因此 $\text{Dina}$ 会立即返回巢穴并结束狩猎。在狩猎点 $2$ 捕获猎物的概率为 $0.50$，即有 $50\%$ 的概率会捕捉到猎物，但由于狩猎点 $2$ 没有其他狩猎点与之直接连通，因此不管在狩猎点 $2$ 是否捕获到猎物，$\text{Dina}$ 都会选择立即返回巢穴，在返回巢穴时，已经消耗 $10$ 体力，根据题意，不管 $\text{Dina}$ 是否已经捕捉到了猎物，她都会结束狩猎。由于是随机选择，故在巢穴时选择狩猎点 $1$ 和 $2$ 进行狩猎的概率均为 $50\%$，根据计算可知，进行一次狩猎所消耗的体力和花费时间的平均值分别为 $7.5=(2+1+2) \times 50\%+(4+2+4) \times 50\%$ 和 $10.5=(3+2+3) \times 50\%+(5+3+5) \times 50\%$。 ------------ **数据范围** - Subtask $1$：$n=1$，$10$ 分。 - Subtask $2$：$1 \le n \le 20$，每个狩猎点和其他狩猎点均无直接道路相连，$20$ 分。 - Subtask $3$：无特殊限制，$70$ 分。 对于 $100\%$ 的数据，$1 \le n \le 200$，$1 \le h_i \le 10$，$1 \le t_i \le 10$，$0 \le p_i \le 1$，$1 \le m \le \text{min}(n (n+1) / 2$，$2000$)，$1 \le h_{u,v} \le 20$，$1 \le t_{u,v} \le 20$，$1 \le H \le 200$，$1 \le T \le 200$。 ------------ **约定** - 地点 $u$ 和地点 $v$ 之间至多有一条直接连接的双向道路，两个地点之间的直连双向道路不会重复给出。 - 忽略 $\text{Dina}$ 进行评估所需要的时间。 - 在输入中，表示概率 $p_i$ 的数值是一个具有两位小数的实数。