P7680 [COCI 2008/2009 #5] JAGODA

Slavko 养了 $n$ 只兔子，他每天用各种水果和蔬菜喂兔子。然而，兔子最喜欢草莓。草莓在隆冬时节很难找到，而且很贵，所以 Slavko 只给部分兔子吃草莓。Slavko 把兔子编号为 $1\sim n$。为了帮助追踪每只兔子得到多少草莓，他决定采用以下草莓分配程序。 Slavko 每天都会买 $S$ 个草莓，然后选一个兔子 $A$ ，然后给它第一个草莓。之后，兔子 $A+1$ 会得到第二个草莓，兔子 $A+2$ 会得到第三个，以此类推。 给每只兔子分配一个最初为空的火柴盒，然后把这 $n$ 个火柴盒排成一排。设 $k$ 为使得 $k^2\leqslant n$ 的最大整数。这样就可以把兔子分成 $\left\lceil\dfrac{n}{k}\right\rceil$组，每组 $k$ 个火柴盒（从第一个开始，最后一组有可能不足 $k$ 个），每组火柴盒旁边也会有一个杯子。我们说 $k$ 个连续的火柴盒和它们的杯子形成一组。 在给兔子草莓之后，Slavko 会把一根火柴放进每个得到草莓的兔子的火柴盒里，**除非**他把火柴放进一组里所有的火柴盒里。此时他不会把火柴放在一组的所有火柴盒里，而是把一根火柴放在这一组所在的杯子里。通过这种方式，兔子收到的草莓总数可以用火柴盒里的火柴数加上杯子里的火柴数来计算。例如，假设 Slavko 有 $11$ 只兔子，即 $n=11$。数字 $3$ 是使得 $k^2\leqslant n$ 的最大整数 $k$，因此 $k=3$。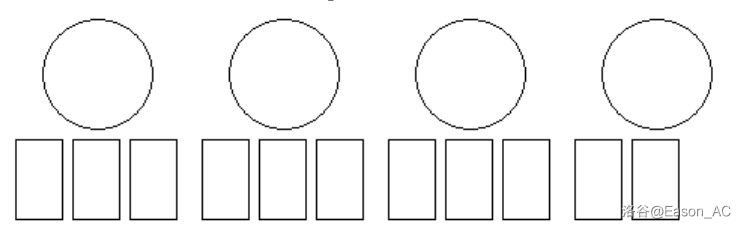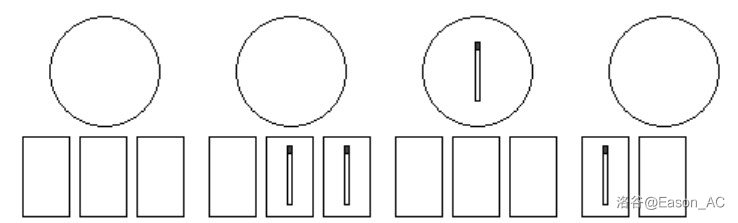因此这些兔子将会被分成四组（最后一组只有两只兔子和两个火柴盒），自然就会有四个杯子，如下图所示：  如果 Slavko 买了 $6$ 个草莓，把第一个送给兔子 $5$，杯子和火柴盒里的状态将变为如下图所示：  现在，请你编写一个程序，给定兔子的数量 $n$、天数 $m$ 以及 $m$ 天中的每一天购买的草莓数量 $S$ 和得到第一个草莓的兔子编号 $A$。对于每一天，输出 Slavko 当天使用的所有火柴盒和杯子中的火柴总数。

输入共 $m+1$ 行。 第一行两个整数 $n,m$，分别表示兔子的总数（也是火柴盒数）和天数。 随后 $m$ 行，第 $i$ 行两个整数 $S,A$，分别表示第 $i$ 天购买的草莓数量和得到第一个草莓的兔子编号。

输出共 $m$ 行，第 $i$ 行一个整数，表示 Slavko 第 $i$ 天使用的所有火柴盒和杯子中的火柴总数。

**【样例 1 解释】** 对于样例 $1$，兔子、火柴盒和杯子摆放的情况即为题面中所给出的例子。 第一天即为题面中所给出的例子，因此 Slavko 第一天放入 $4$ 根火柴。 第二天 Slavko 买了 $3$ 个草莓，并将第一个草莓给了 $1$ 号兔子，这样的话，$1$、$2$、$3$ 号兔子都得到草莓，由于它们三个兔子都在一组里面，所以 Slavko 只需要在第 $1$ 个杯子里面放入一根火柴。因此 Slavko 第一天放入 $1$ 根火柴。 第三天，Slavko 可以给他所有的兔子送草莓，所以需要在每个杯子里放一根火柴。总共是把 $4$ 根火柴放到杯子里，他在这天使用的杯子里（就是所有杯子）在他放置后一共有 $6$ 根火柴，所以输出 $6$。 **【数据范围】** 对于所有数据。$1\leqslant n,m\leqslant 10^5$，$1\leqslant A\leqslant n$，$1\leqslant A+S-1\leqslant n$。 **【题目来源】** 本题来源自 **_[COCI 2008-2009](https://hsin.hr/coci/archive/2008_2009/) [CONTEST 5](https://hsin.hr/coci/archive/2008_2009/contest5_tasks.pdf) T3 JAGODA_**，按照原题数据配置，满分 $70$ 分。 由 [Eason_AC](https://www.luogu.com.cn/user/112917) 翻译整理提供。