P7697 [COCI 2009/2010 #4] OGRADA
题目背景
Matjia 需要粉刷他的旧篱笆。
题目描述
篱笆是由 $n$ 块木板做成的,每块木板宽 $1$ 厘米,高度不一。为了方便快捷,他给自己买了一个宽 $x$ 厘米的超级油漆辊。然而超级油漆辊来了一个陷阱——Matija 必须始终使辊子紧密地整个接触木板,否则油漆会滴到四周并污渍所有东西。此外,辊子必须始终与地面平行,以防泄漏。这意味着为了让 Matija 安全地使用压路机,他需要选择 $x$ 块木板,并从最下面的木板的底部到顶部一次涂上油漆。然后,他选择一些其他的木板,油漆它们,以此类推。
这使得一些木板的部分没有上漆。Matija 必须用牙刷刷这些部分。这显然是相当乏味的,所以他请你帮他编写一个程序,求出他需要手动刷漆的最小面积。因为有不止一种方法可以做到这一点,他也想知道需要使用超级油漆辊的最少次数。
输入格式
输入共两行。
第一行两个整数 $n,x$,分别代表木板的个数和超级油漆辊的宽度。
第二行 $n$ 个正整数 $h_1,h_2,\dots,h_n$,表示每个木板的高度。
输出格式
输出共两行。
第一行一个整数,表示 Matjia 需要手动刷漆的最小面积。
第二行一个整数,表示在手动刷漆的面积最小的前提下,需要使用超级油漆辊的最少次数。
说明/提示
**【样例 1 解释】**
对于样例 $1$,Matjia 需要使用两次超级油漆辊。
- 第一次,用超级油漆辊粉刷第 $1,2,3$ 个木板,粉刷高度为 $3\text{ cm}$,因此粉刷面积为 $9\text{ cm}^2$。
- 第二次,用超级油漆辊粉刷第 $3,4,5$ 个木板,粉刷高度为 $4\text{ cm}$,因此粉刷面积为 $12\text{ cm}^2$。
因为两次粉刷有 $3\text{ cm}^2$ 的面积重叠,因此剩下的需要手动粉刷的面积为 $5+3+4+4+5-9-12+3=3\text{ cm}^2$。可以证明这样的方案需要手动粉刷的面积是最小的并且使用超级油漆辊的次数也是最少的。
具体可以结合下图理解:
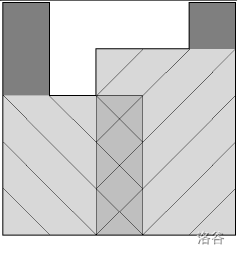
**【数据范围】**
对于所有数据,$1\leqslant n\leqslant 10^6$,$1\leqslant x\leqslant 10^5$,$1\leqslant h_i