P7728 旧神归来(Return of Them)
题目背景
随着虚影与暗影的决战、月岛祭坛的完工、天体风暴的出现、天界捍卫者的到来,一切月球与远古的秘密仿佛已经行至终局。
旧神即将归来!
题目描述
月岛上的一棵普通的树在月光侵蚀的影响下不断生长,随着月面风暴的来临变得更加无限制。
具体地,生长规则如下:
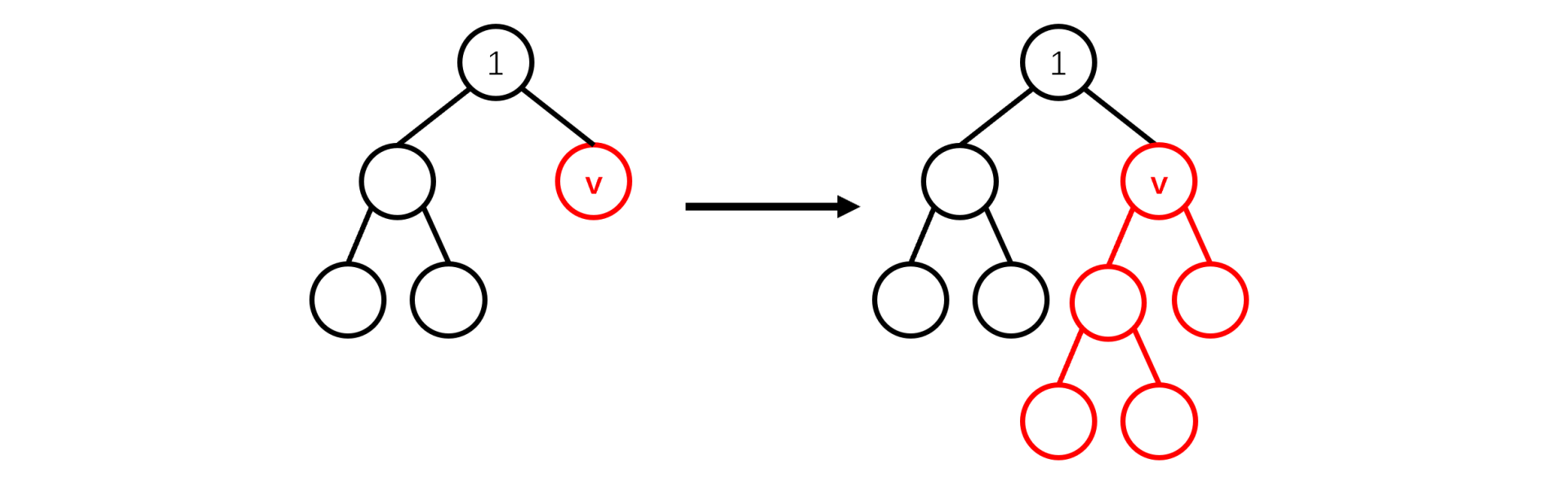
- 初始有一棵包含 $n$ 个结点的以 $1$ 为根的**有根树** $T_0$;
- 在第 $i$ 天,树将从 $T_{i - 1}$ 生长为 $T_i$,生长规则为:令 $v$ 是 $T_{i - 1}$ 中**深度最小的叶结点**(若有多个则任意选择一个),以 $v$ 这个点替换成 $T_{i - 1}$ 本身。
本题中一个结点的深度定义为它到根结点的简单路径所经过的**边数**,注意这可能与常规定义不同。
下图展示了一个从 $T_{i-1}$ 生长到 $T_i$ 的例子:
除了面对天界捍卫者,对于环境效应的估计也是重要的,所以你需要计算:
- 对于每个整数 $d \in [1, m]$,求出 $S_d$ 表示最小的天数,满足 $T_{S_d}$ 中深度最小的叶结点深度**大于** $d$。
答案对 $998244353$ 取模。
输入格式
第一行,两个整数 $n, m$,分别表示 $T_0$ 的结点数和要求答案的深度范围。
接下来 $n - 1$ 行,每行两个整数 $x, y$,表示 $T_0$ 中结点 $x, y$ 间有一条边。
输出格式
输出 $m$ 行,第 $i$ 行输出一个整数表示 $S_i$。
说明/提示
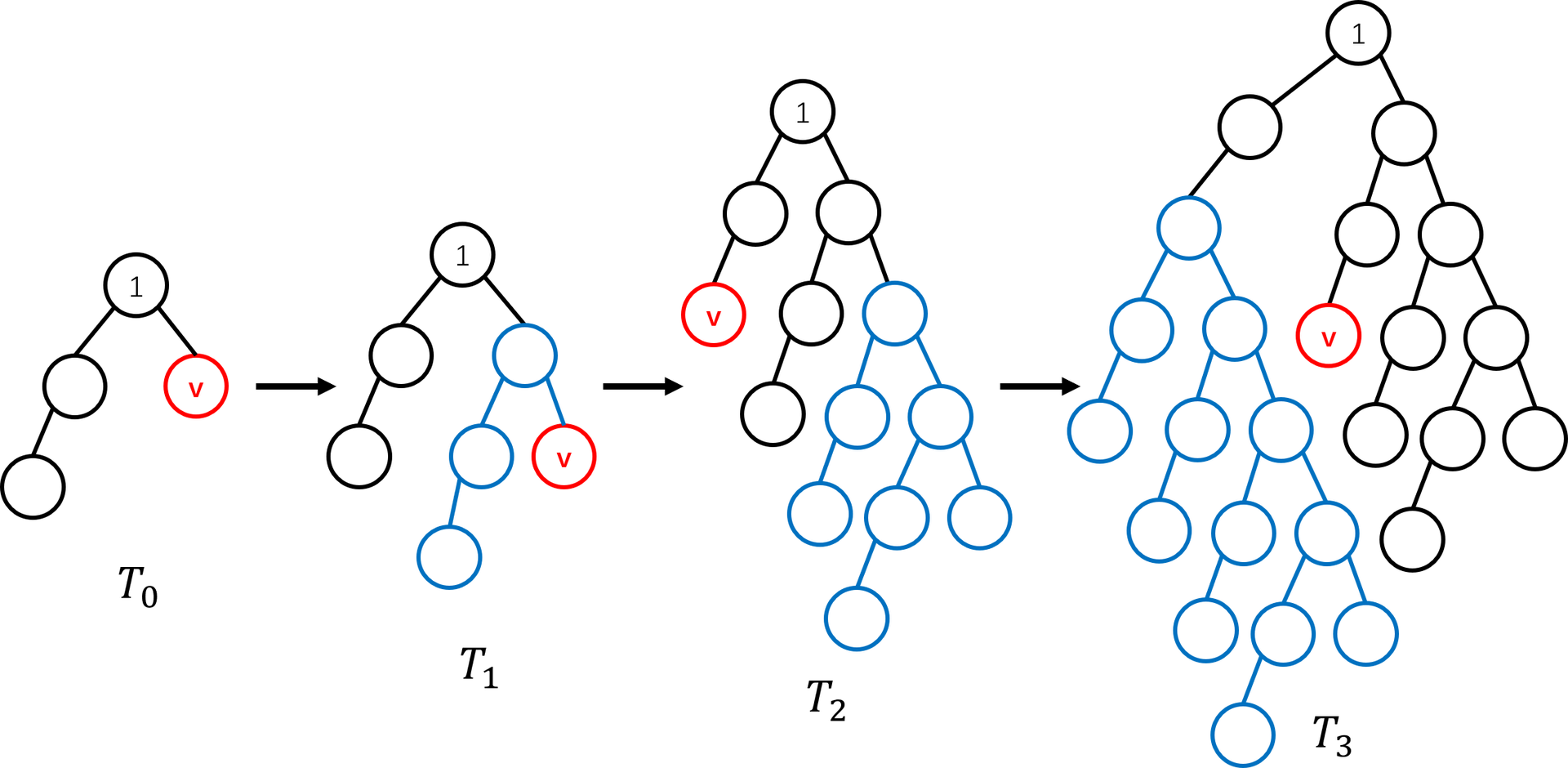
**【样例 1 解释】**
如图展示了 $T_0$ 至 $T_3$ 的形态,最浅的叶子由红色标出,上一次生长出的部分用蓝色标出。
可以看到,$T_1$ 中深度最小的叶子深度大于 $1$,$T_3$ 中深度最小的叶子深度大于 $2$,而再操作一次后得到的 $T_4$ 中深度最小的叶子深度就会大于 $3$(应为 $4$),这是对样例输出前三行的一个解释:
---
**【数据范围】**
**本题采用捆绑测试。**
对于 $100 \%$ 的数据:$2 \le n, m \le {10}^5$。
| 子任务编号 | 分值 | $n, m \le$ | 特殊限制 |
|:-:|:-:|:-:|:-:|
| $1$ | $12$ | $10$ | $T_0$ 为二叉树 |
| $2$ | $8$ | ${10}^5$ | $T_0$ 为以 $1$ 为一端的链 |
| $3$ | $25$ | ${10}^5$ | $T_0$ 为二叉树,且每个非叶结点都有两个子结点 |
| $4$ | $10$ | $100$ | 无 |
| $5$ | $12$ | $1000$ | 无 |
| $6$ | $15$ | $30000$ | 无 |
| $7$ | $18$ | ${10}^5$ | 无 |
---
