P7784 「MCOI-Zero / AC6-M15」 Chandelier
题目背景
「不,还没完……」
「什么!?」
「炮管打开了。
那个丑陋的东西开始通过炮管散热了!」
「它的关键区域就在炮管后面。」
「Talisman……
……我们可以信任你,对吗?」
$$_{{\frac{\large\text{ACE COMBAT }\Large6}{\tiny{\text{F i r e s\quad O f\quad L i b e r a t i o n}}}}}\\ \text{Mission 15} \\\Large\text{Chandelier}\\\tiny -\textit{ To All Things }
-$$

题目描述
Chandelier 的核心可以被描述为一个 $n\times m$ 的矩阵。初始时,矩阵中的每一个格子都是一个独立的空间。
如果在核心中存在两个空间使得它们在矩阵上的并是一个矩形,则这两个空间可以合并为一个空间,合并出的空间就是原先两个空间的并。
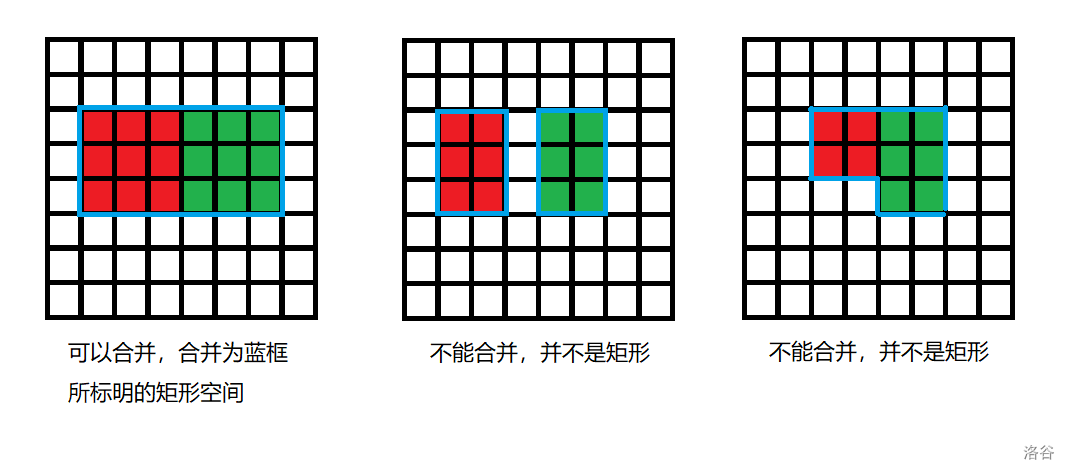
如果不存在任何两个空间的并是矩形,则我们称核心达到了稳定状态。
如果一个空间的长达到了 $n$ 或者宽达到了 $m$,那么核心将会短路,引发爆炸。**注意这里空间的长指的是和原矩阵的长为 $n$ 的边平行的边的长度,宽类似。也就是说如果平行于 原矩形的长为 $n$ 的边 的边长达到了 $m$ 且 $m
输入格式
一行用空格分割的两个整数 $n,m$。
输出格式
如果无解,输出一行 `-1`。
如果有解,在第一行输出一个整数 $x$,表示空间数量。
然后输出一个 $n\times m$ 的矩阵 $a$,满足 $1\leq a_{i,j}\leq x$。$a_{i,j}$ 表示 $(i,j)$ 属于哪一个空间。相同的数代表相同的空间,不同的数代表不同的空间。
如果有多解,输出任意一个即可。
说明/提示
- Subtask 1(20 pts):$n,m\leq 2$。
- Subtask 2(40 pts):$n,m\leq 4$。
- Subtask 3(40 pts):无特殊限制。
对于 $100\%$ 的数据,满足 $1\leq n,m\leq 10^{3}$。
idea:Sol1,solution:Sol1,code:Sol1,data:Sol1
---
「我看见大炮终于完了……」
「全机注意,
战争结束了。」
……
「Talisman 看,太阳升起来了。」
「尽管黑夜是如此漫长,但终将迎来黎明的曙光。」
「我们失去的战友,都把他们的生命之火
献给了破晓之光。」
「我们尽最大努力存活——
就是对他们的最好悼念。」
「现在,来吧。」
「让我们回家吧。」