P7802 [COCI 2015/2016 #6] SAN

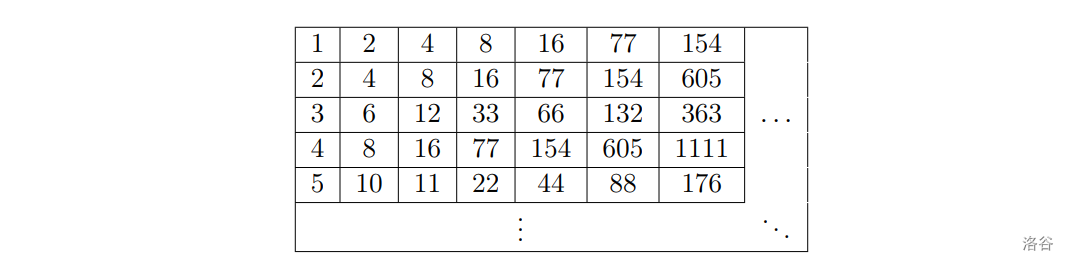
$\text{Anica}$ 有一张神秘的无限表，表里有无限行和无限列。有趣的是，表中的每个数字出现的次数是有限的。 定义函数 $\mathrm{rev}(i)$，返回 $i$ 在十进制下翻转后得到的新数字。例如 $\mathrm{rev}(213)=312$，$\mathrm{rev}(406800)=008604=8604$。 表中第 $i$ 行第 $j$ 列的数字 $A(i,j)$ 由以下方式得到： - $A(i,1)=i$ - $A(i, j) = A(i, j − 1)+\mathrm{rev}\big(A(i,j-1)\big)$，$j>1$  现在 $\text{Anica}$ 给出 $Q$ 个询问，每个询问给出两个整数 $L$ 和 $R$，请你求出无限表中有多少个数的大小在 $\big[L,R\big]$ 中。

第一行包含一个整数 $Q$。 接下来 $Q$ 行，每行包含两个整数 $L$ 和 $R$。

输出包含 $Q$ 行，每行一个整数，其中第 $i$ 行为第 $i$ 个问题的答案。

**【数据范围】** 对于 $50\%$ 的数据，保证 $1\le L,R\le 10^6$。 对于 $100\%$ 的数据，保证 $1\le Q\le 10^5$，$1\le L,R\le 10^{10}$。 **【题目来源】** **题目译自 [COCI 2015-2016](https://hsin.hr/coci/archive/2015_2016/) [CONTEST #6](https://hsin.hr/coci/archive/2015_2016/contest6_tasks.pdf) T6 SAN**。 **本题分值按 COCI 原题设置，满分 $160$**。