P7806 冰魄吐息

[$\text{加强版}\Leftarrow$](/problem/U174529)

$N$ 个点，第 $i$ 个点坐标为 $(x_i,y_i)$。 定义一束激光：$y=kx$，若点 $i$ 满足到该条直线距离 $\le d$，认为被激光击中。 求使用至多 $K$ 束激光，击毁图中所有点的最小代价 $d$。

第一行输入两个正整数 $N,K$。 第 $2 \sim N+1$ 行，每行两个非负整数 $x_i,y_i$，表示第 $i$ 个点的坐标。

第一行输出最小代价 $d$，保留到小数点后 $2$ 位。

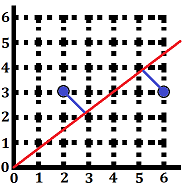
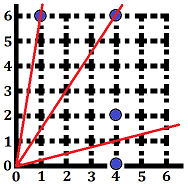
#### 样例说明 |  |  | | :----------- | :----------- | | 样例 $\#1$ 中两蓝色点坐标分别为 $(2,3)$ 和 $(6,3)$，到直线 $y=\frac{3}{4}x$ 的距离均为 $\frac{6}{5}=1.2$，因此输出 `1.20`。 | 样例 $\#2$ 中坐标为 $(4,0),(4,2)$ 的点与斜率为 $\frac{1}{4}$ 的直线之间距离为 $\frac{4}{17}\sqrt{17}\approx0.97014\dots$，因此输出 `0.97`。 | 可以证明两个样例中的方案是最优的，因此所求的 $d$ 是最小的。 #### 提示 1. 可能会用到的公式：点 $(x_0,y_0)$ 到直线 $y=kx$ 的距离是 $\dfrac{|y_0-kx_0|}{\sqrt{k^2+1}}$。 2. 对于 C++ 选手，**建议使用** 变量类型 `long double` 进行数值计算。 输出时请用形如 `printf("%.2Lf",ans)` 的形式输出答案，注意 `%.2Lf` 中的 L 是大写。 3. 本题中存在的浮点数运算可能较多，虽然已经增大时限，但仍然请注意常数因子对程序效率的影响。 #### 数据范围 **本题采用捆绑测试**。 记 $M$ 为所有 $x_i,y_i$ 的最大值。 | Subtask | Score | $M\le$ | $K\le$ | | :----------: | :----------: | :----------: | :----------: | | $1$ | $30$ | $10$ | $1$ | | $2$ | $30$ | $1.5\times10^4$ | $1$ | | $3$ | $40$ | | | 对于 $100\%$ 的数据：$1\le N,M,K\le2.5\times10^4$。 所有数据均保证不存在相同的 $(x_i,y_i)$ 出现多次。 --- ### 后记 冰魄战龙我吹爆 $\sim$ 如果您也热爱 ddt，请在比赛结束后找到出题人，并把他虐一顿。  出题人推荐阅读题解：（优点：显然）https://www.luogu.com.cn/blog/_post/362493