P7892 『JROI-3』田径

你准备玩起 MC。

你需要用栅栏框住一个长方形区域，假设这个长方形区域大小为 $a \times b$ 个像素格，则需要长为 $a+1$，宽为 $b+1$ 规模的栅栏框住这个区域。 现在你发现他的羊和牛需要**恰好** $n$ 个像素格才够生存，而你的背包里有 $m$ 个栅栏，你想知道，你用你所拥有的的栅栏是否能框出 $n$ 个像素格？ 不需要用光所有栅栏，只要框出区域大小为 $n$ 个像素格的长方形即可。 注意，上面的 $a,b,n,m$ 都应是整数。

第一行一个整数 $T$，表示测试组数。 接下来 $T$ 行，一行两个整数 $n,m$，同题意。

一行一个字符串，如果可行输出 `Good`，如果不可行输出 `Miss`。

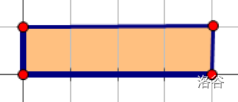
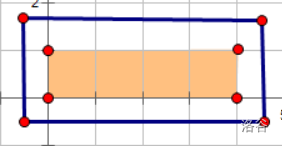
#### 样例 1 解释 第一组数据： 实测可证，无法用 $1$ 个栅栏围出 $4$ 个像素格。 第二组数据： 可以考虑围出如下 $4=1 \times 4$ 的像素格。  用下方的方式只需要用 $14$ 个栅栏即可。  栅栏宽为 $1+1=2$，长为 $4+1=5$，$(2+5) \times 2=14$。 #### 数据规模与约定 **本题采用捆绑测试。** - Subtask 1（30 pts）：$1\le n,m \le 10^4$，$T \leq 10^3$； - Subtask 2（70 pts）：$1\le n,m \le 10^{8}$，$T \leq 10^3$。 ---- 在本题中栅栏是**抽象化**的而非具象化的，即栅栏将会**退化成一个点而非一个方格**，也就是我们可以通过**求周长的方式**求出一个栅栏框所需消耗的栅栏（如果不理解可以看看样例 1 解释）。