P7920 [Kubic] Permutation
题目背景
建议先看 E 题题目背景。
题目描述
对于一个 $1\sim n$ 的排列 $p$,定义 $G_p$ 为使用以下方法构造出来的**无向图**:
- 对于每一个 $i\in (1,n]$,找到最大的 $j\in [1,i)$ 满足 $p_i>p_j$,然后连一条 $i,j$ 之间的边,如果不存在这样的 $j$ 则不连。
给定一棵有 $n$ 个节点的树 $T$。
把 $p$ 称为**好排列**当且仅当 $G_p$ 与 $T$ 同构。
如果存在**好排列**,输出其中**字典序最大**的一个。否则输出 $-1$。
无向图 $G_1,G_2$ 同构当且仅当存在一个 $1\sim n$ 的排列 $q$,满足 $\forall (u,v)\in G_1,(q_u,q_v)\in G_2,\forall (u,v)\notin G_1,(q_u,q_v)\notin G_2$。
输入格式
第一行,一个整数 $n$。
接下来 $n-1$ 行,每行两个整数 $u,v$,表示 $u,v$ 之间有一条边。
输出格式
共一行,$n$ 个整数,表示答案;或一个数 $-1$,表示无解。
说明/提示
对于 $100\%$ 的数据,$1\le u,v\le n\le 5\times 10^3$。
||分值|$n$|特殊性质|
|:-:|:-:|:-:|:-:|
|$\operatorname{Subtask}1$|$15$|$\le 8$|无|
|$\operatorname{Subtask}2$|$5$|无特殊限制|树退化为一条链|
|$\operatorname{Subtask}3$|$15$|无特殊限制|度数 $\ge 3$ 的节点个数 $\le 1$|
|$\operatorname{Subtask}4$|$20$|$\le 100$|无|
|$\operatorname{Subtask}5$|$20$|$\le 10^3$|无|
|$\operatorname{Subtask}6$|$25$|无特殊限制|无|
**说明:样例解释中的节点编号是 $p$ 中的下标。**
### 样例解释 1
$G_p$ 的形态如下:
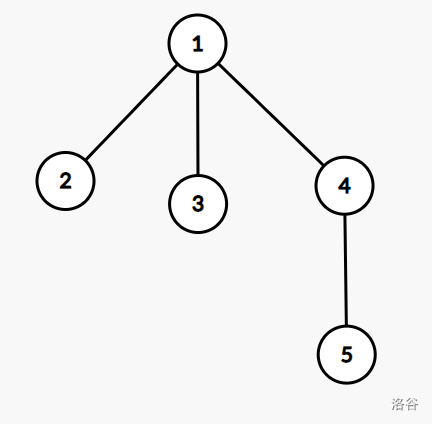
可以证明没有更优的方案。
### 样例解释 2
$G_p$ 的形态如下:
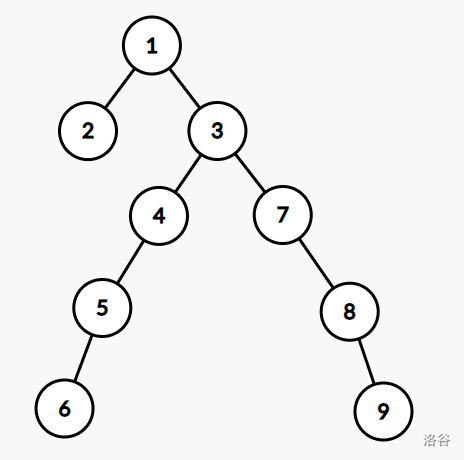
可以证明没有更优的方案。