P7945 「Wdcfr-1」Yet Another Cirno Game (easy version)

**The only difference between the two versions is whether you have to find a way to get the maximum points.** Cirno drew a graph. This graph contains $4\cdot n$ nodes, numbered $0$ through $4\cdot n - 1$. Also: - For any $0\le i\le 3$ and $0 \le j, k \lt n$, node $(n\cdot i + j)$ and node $(n\cdot i + k)$ are connected. - For any $0 \le i < n$ and $0 \le j, k \le 3$, node $(i + n\cdot j)$ and node $(i + n\cdot k)$ are connected. Cirno called Daiyousei to come and play with her. The rules for this game are as follows: - Firstly, Cirno chooses $2\cdot n$ (i.e. half) of the nodes, and she colors them blue. The rest are left red. - Then there are $2\cdot n$ turns: for each turn Cirno first chooses a blue node, and Daiyousei chooses a red node. If those two nodes are connected, Daiyousei gets a point. Try to maximize the number of points Daiyousei gets.

The first line contains an integer $n$. Then one line below, $2\cdot n$ numbers follow: they are the nodes that Cirno chose.

For each test case, output an integer $x$ in a single line, which is the maximum number of points Daiyousei can get. You don't have to output anything else in this version.

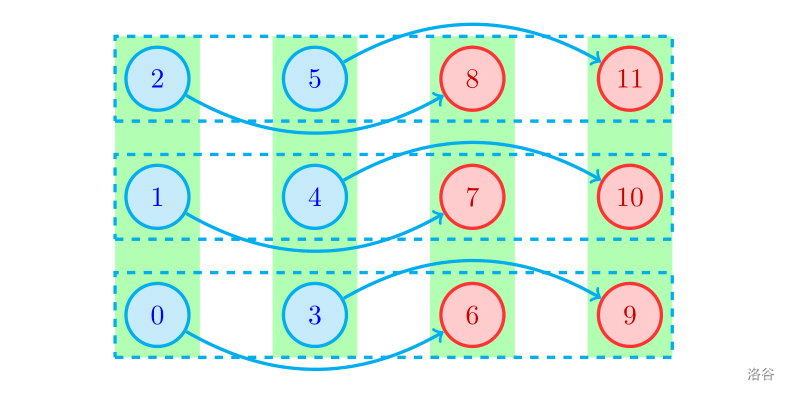
### Explanation In the following picture, nodes in matrices are connected to each other. Cirno chose nodes $0,1,2,3,4,5$. Arrows below show a possible way for Daiyousei to get the maximum number of points she can get.  ### Constraints $1\le n\le 2\times 10^6$.