P7946 「Wdcfr-1」Yet Another Cirno Game (hard version)

**The only difference between the two versions is whether you have to find a way to get the maximum points.** Cirno drew a graph. This graph consists of $4\cdot n$ nodes, which are numbered $0$ through $4\cdot n - 1$. Also: - For $0\le i\le 3$ and $0 \le j, k \lt n$, node $(n\cdot i + j)$ and node $(n\cdot i + k)$ are connected. - For $0 \le i \le n$ and $0 \le j, k \le 3$, node $(i + n\cdot j)$ and node $(i + n\cdot k)$ are connected. Cirno called Daiyousei to come and play with her. The rules for this game are as follows: - Firstly, Cirno chooses $2\cdot n$ (i.e. half) of the nodes, and she colors them blue. The rest are left red. - Then there are $2\cdot n$ turns: for each turn Cirno first chooses a blue node, and Daiyousei chooses a red node. If those two nodes are connected, Daiyousei gets a point. Try to maximize the number of points Daiyousei gets.

In the first line, $n$ is provided. In the second line, $n$ numbers follow: they are the nodes that Cirno chose.

In the first line output $x$, which is the maximum number of points Daiyousei can get. Then output $2\cdot n$ integers. For each node that Cirno chooses, output the corresponding node that Daiyousei responds with. Obviously the order of the chosen nodes doesn't matter. The solution must get the maximum number of points possible.

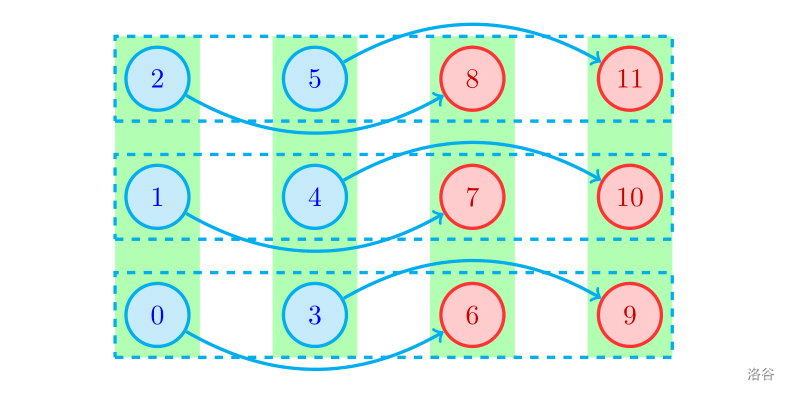
### Explanation In the following picture, nodes in matrices are connected to each other. Cirno chose nodes $0,1,2,3,4,5$. Arrows below show a possible way for Daiyousei to get the maximum number of points she can get.  ### Constraints $1\le n\le 2\times 10^6$.