P7970 [KSN2021] Binary Sea
题目描述
有一个 $N\times M$ 的网格,行列从 $0$ 开始,从左上到右下编号。
第 $i$ 行,第 $j$ 列的格子是黑格当且仅当 $i\text{ and }j=0$。
两个黑格联通当且仅当它们都是黑格且它们可以经过若干个有**邻边**的黑格到达。
给定 $Q$ 个矩形,左上角为 $(x_1,y_1)$,右下角为 $(x_2,y_2)$,你需要对于每个矩形求出所有的黑格形成了多少连通块。
输入格式
第一行输入三个整数 $N,M,Q$,代表网格大小和询问数量。
接下来 $Q$ 行,每行输入四个整数 $x_1,y_1,x_2,y_2$,代表询问矩形。
输出格式
对于每组数据输出一行,包含一个整数,代表答案。
说明/提示
**【样例解释】**
以下为样例中四个询问的图示:
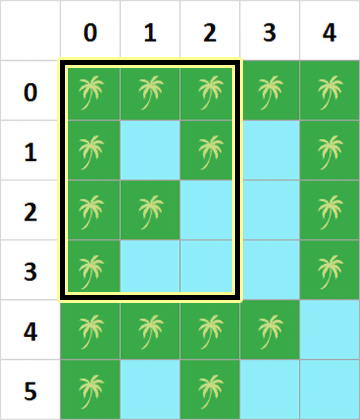 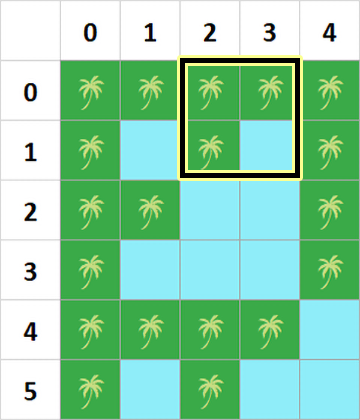  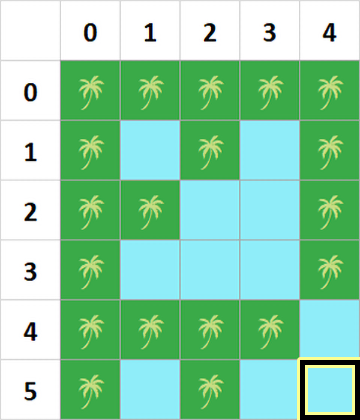
**【数据范围】**
**本题采用捆绑测试。**
* Subtask 1(5 points):只存在一组数据,满足 $N = M=12$,$Q=3$,每次询问的 $(x_1,y_1,x_2,y_2)$ 依次为 $(1,1,9,8)$,$(8,8,11,11)$ 和 $(4,3,5,9)$。
* Subtask 2(11 points):$N,M,Q\le 200$。
* Subtask 3(10 points):$N,M,Q\le 2000$,$x_1=x_2$。
* Subtask 4(20 points):$N,M,Q\le 2000$。
* Subtask 5(4 points):$x_1=x_2=0$。
* Subtask 6(6 points):保证对于每个询问存在整数 $k$ 使得 $x_1=x_2=2^k$。
* Subtask 7(29 points):$x_1=x_2$。
* Subtask 8(15 points):无特殊限制。
对于所有数据,$0\leq x_1\leq x_2