P7980 [JRKSJ R3] a question

这是一个问题。

现在有一棵 $n$ 个结点的树 $\text{T}$，边带权，结点的编号为 $[1,n]$ 的排列。 设 $\text{G}$ 为 $\text{T}$ 的补图。对于 $\text{G}$ 上的每一条边 $(x,y)$，该边的权值为 $\text{T}$ 上 $x\rightarrow y$ 的路径上的边权和。 设 $dis(x,y)$ 为 $\text{G}$ 上 $x,y$ 两点之间的最短路径的长度。若 $x,y$ 两点不连通，则令 $dis(x,y)=0$。 求 $\displaystyle\sum_{i=1}^{n-1} \sum_{j=i+1}^n dis(i,j)$。

输入的所有数都为整数。 第一行一个数 $n$。\ 接下来 $n-1$ 行每行三个数 $u,v,w$ 表示 $\text{T}$ 中有一条连接 $u,v$ 且边权为 $w$ 的边。

输出一个数表示答案，由于答案很大，请对 $10^9+7$ 取模。

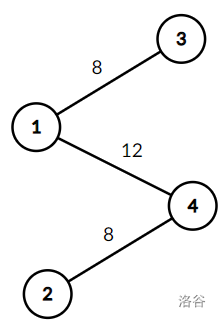
$\text{T}$ 的补图 $\text{G}$ 的定义为：对于边 $(x,y)(1\le x,y\le n,x\ne y)$，若 $\text{T}$ 中不存在该边 ，则 $\text{G}$ 中存在该边；若 $\text{T}$ 中存在该边 ，则 $\text{G}$ 中不存在该边。$\text{G}$ 为无向图。 ### 样例解释 对于样例 $2$，图 $\text{G}$ 如图所示：  我们有： | $dis(i,j)$ | $j=1$ | $j=2$ | $j=3$ | $j=4$ | | :----------: | :----------: | :----------: | :----------: | :----------: | | $i=1$ | | $20$ | $8$ | $12$ | | $i=2$ | | | $28$ | $8$ | | $i=3$ | | | | $20$ | 所以答案为 $96$。 ### 数据规模 | $\text{Subtask}$ | $n\le$ | 特殊性质 | 分值 | 子任务依赖 | | :----------: | :----------: | :----------: | :----------: | :----------: | | $1$ | $10^3$ | 无 | $10$ | 无 | | $2$ | $10^4$ | 无 | $20$ | $1$ | | $3$ | $2\times 10^6$ | 树为菊花 | $20$ | 无 | | $4$ | $2\times 10^6$ | 树为链 | $20$ | 无 | | $5$ | $2\times 10^6$ | 无 | $30$ | $1,2,3,4$ | 对于 $100\%$ 的数据，$2\le n \le 2\times 10^6$，$1\le x,y\le n$，$0\le v\le 10^9$。 **本题输入文件较大，请使用恰当的读入方式。**