P8063 [BalkanOI 2012] Shortest paths

Bit 镇的你要去 Hex 镇找你的 npy。

你所在的国家有 $n$ 个镇（镇从 $1$ 到 $n$ 编号），$m$ 条双向道路，Bit 镇在 $a$ 点，Hex 镇在 $b$ 点。每条道路有一个长度。你很了解周围的地图，所以找到了两个镇之间的最短路径，而且，决定将这条路径称为幸运路径。 有一天，政府决定在公路上施工，为了维持交通，决定每次只关闭一条道路（关闭后道路不可通行）。 对于这条幸运路径上的每一条道路，你想知道当这条道路正在关闭时从 Bit 镇到 Hex 镇的最短距离。

输入的第一行由 4 个整数组成：$n,m,a,b$，分别表示城镇数量，道路数量，Bit 镇编号，Hex 镇编号。 接下来的 $m$ 行，第 $i$ 行包含三个整数 $u_i,v_i,w_i$ ：城镇 $u_i$ 和城镇 $v_i$ 由长度为 $w_i$ 的道路连接。 输入的最后一行由数字 $k$ 和 $k$ 个数字组成：$(v_1(=a),v_2,\dots,v_{k}(=b))$ ，表示幸运路径。 $v_i(1\le i\le k)$ 表示幸运路径上的第 $i$ 个点的编号。

输出共 $k-1$ 行。 对于每个 $t=1\dots k-1$，输出一行一个整数：道路 $(v_t,v_{t+1})$ 施工时，Bit 镇和 Hex 镇之间的最短路径的长度。如果路径不存在，则输出 `-1`。

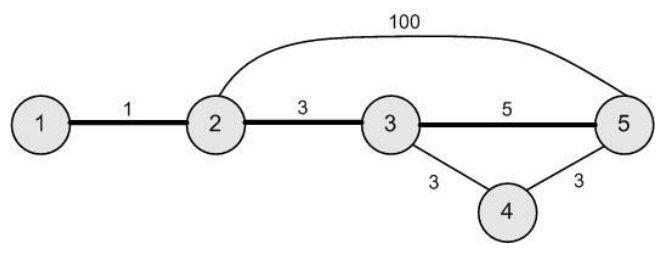
#### 数据范围： Subtask#0 为样例。 $1\le n\le 2000$，$1\le m\le10^5$，$1\le u_i,v_i\le n$，$1\le w_i\le10^5$。 对于 $i\neq j$，满足 $u_i\neq u_j$ 或 $v_i\neq v_j$。 #### 样例解释：  封闭道路 $(1,2)$ 后从点 $1$ 的 Bit 镇无法到达点 $5$ 的 Hex 镇。 封闭道路 $(2,3)$ 后从点 $1$ 的 Bit 镇到点 $5$ 的 Hex 镇的最短路为 $1\rightarrow 2\rightarrow5$，长度 $1+100=101$。 封闭道路 $(3,5)$ 后从点 $1$ 的 Bit 镇到点 $5$ 的 Hex 镇的最短路为 $1\rightarrow 2\rightarrow3\rightarrow4\rightarrow5$，长度 $1+3+3+3=10$。