P8067 [BalkanOI 2012] balls
题目背景
你在玩物理画线。
题目描述
有 $N$ 个球和 $N$ 个杯子,从左到右编号依次为 $1\dots N$。开始时第 $i$ 个球对准第 $i$ 个杯子(不受影响的情况下第 $i$ 个球落入第 $i$ 个杯子)。第 $i$ 个杯子有一个分值 $c_i$,一个球落入一个杯子可以获得该杯子的分数(杯子容量视为无限),分数可能为负数。
你可以画两种线,线的两端点必须对准某个杯子,且两个端点不能是同一个杯子:
1. 从左上到右下,设左上对准的杯子编号为 $i$,右下对准的杯子编号为 $j$,使编号为 $i\dots j$ 的球全部落入第 $j$ 号杯子。
1. 从右上到左下,设左下对准的杯子编号为 $i$,右上对准的杯子编号为 $j$,使编号为 $i\dots j$ 的球全部落入第 $i$ 号杯子。
现在你想知道你只用**恰好一根**第一种线、**恰好一根**第二种线,分别能获得的最大分数。
输入格式
输入的第一行包含一个整数 $N$。
接下来一行 $N$ 个整数,表示 $c_1\dots c_N$。
输出格式
输出第一行一个整数——只使用第一种的最大分数。
输出第二行一个整数——只使用第二种的最大分数。
说明/提示
#### 数据范围:
Subtask#0 为样例。
$3\le N\le3\times10^5$,$|c_i|\le10^9$。
#### 样例解释:
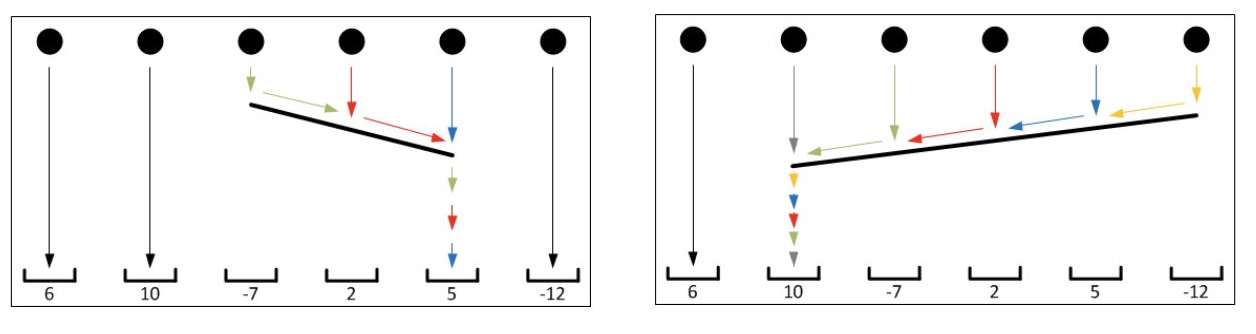
第一幅图为第一种线,分数:$6+10+5+5+5+(-12)=19$,可以证明是最大值。
第二幅图为第二种线,分数:$6+10+10+10+10+10=56$,可以证明是最大值。