P8089 『JROI-5』Color

【被三月删除的图片】 泷泽三月 Orz --- 被删除图片会偷偷展示给报名讲评的同学（

**请注意到并不正常的时间限制。** 小 C 有一棵 $dep$ 层 $n$ 个节点的**完全二叉树**，她希望选择其中一个**包含根节点**的**连通块**染色，她想知道有几种不同的染色方案，答案对 $998,244,353$ 取模。

多测，第一行一个整数 $T$，表示测试组数。 **对于每组数据** 第一行一个整数 $dep$，同题意。 第二行一个整数 $s$，表示最底层叶子结点数目，特别的，他们将用二进制表示，你将读入一个 $dep$ 位 $\texttt{01}$ 串，用以表示 $s$，若转换为二进制后不足 $dep$ 位则用前缀 $0$ 补充。 **保证数据合法。**

对于每组数据，一行一个整数，表示合法的染色方案的个数，需要**换行**。

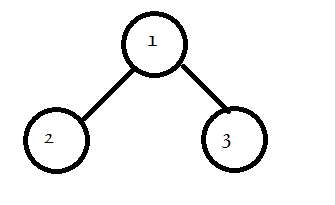
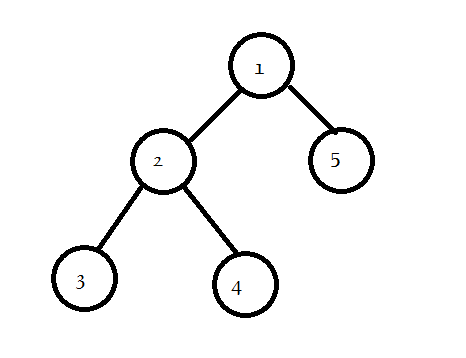
你可以通过学习 [OI-Wiki 树基础](https://oi-wiki.org/graph/tree-basic/) 来了解题面中的名词。 【样例解释】 对于样例 #1，可以画出如下所示二叉树。  我们对该二叉树按照**前序遍历标号**（如图），得到点集 $\left(1,2,3\right)$。 则仅有 $\left(1,2,3\right),\left(1,2\right),\left(1,3\right),\left(1\right)$ 是合法的染色方案。 **** 对于样例 #3，可以画出如下所示二叉树。  我们对该二叉树按照**前序遍历标号**（如图），得到点集 $\left(1,2,3,4,5\right)$。 则仅有 $\left(1,2,3,4,5\right),\left(1,2,3,4\right),\left(1,2,3\right),\left(1,2,4\right),\left(1,2\right),\left(1,2,3,5\right),\left(1,2,4,5\right),\left(1,2,5\right),\left(1,5\right),\left(1\right)$ 是合法的染色方案。 显然 $\left(2,3,4\right),\left(1,3,4\right)$ 不是合法的染色方案，前者没有包含根节点，后者染色的点集不是联通的。 *** 对于 $30\%$ 的数据，$1\leq T\leq 10, 1\leq dep \leq 20$。 对于另外 $20\%$ 的数据，树是满二叉树（即完美二叉树，perfect binary tree）。 对于 $100\%$ 的数据，$1\leq T\leq 10, 1\leq dep \leq 10^6$。