P8127 [BalticOI 2021] The Xana coup (Day2)

给定一棵点数为 $N$ 个树，第 $i$ 个点有点权 $a_i$，$a_i \in \{0,1\}$。 你可以进行切换操作： - 对点 $i$ 进行切换操作会使得点 $i$ 及与其 **直接相连** 的点的点权取反。 其中直接相连指两点之间恰好只有一条边。 求至少需要多少次切换操作才能使得所有点的点权变为 $0$。

第一行一个整数 $N$ 代表树的点数。 接下来 $N-1$ 行每行两个整数代表树的一条边。 第 $N+1$ 行 $N$ 个整数 $a_i$ 代表第 $i$ 个点的点权。

如果有解，一行一个整数代表答案。 如果无解，输出 `impossible`。

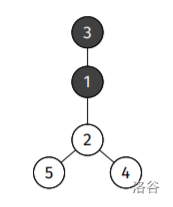
#### 样例 1 解释  $a_i=0$ 为黑色，$a_i=1$ 为白色。 可以对点 $4,5,3,1$ 进行切换操作使得所有点的点权为 $0$。 #### 数据规模与约定 **本题采用捆绑测试。** - Subtask 1（5 pts）：$N \le 20$。 - Subtask 2（15 pts）：$N \le 40$。 - Subtask 3（10 pts）：如果点 $u$ 和点 $v$ 满足 $|u-v|=1$，那么他们有边相连。 - Subtask 4（40 pts）：一个点最多与 $3$ 个点相连。 - Subtask 5（30 pts）：无特殊限制。 对于 $100\%$ 的数据，$3 \le N \le 10^5$。 #### 说明 翻译自 [BalticOI 2021 Day2 C The Xana coup](https://boi.cses.fi/files/boi2021_day2.pdf)。