P8132 [ICPC 2020 WF] Landscape Generator

ICPC2020 WF E

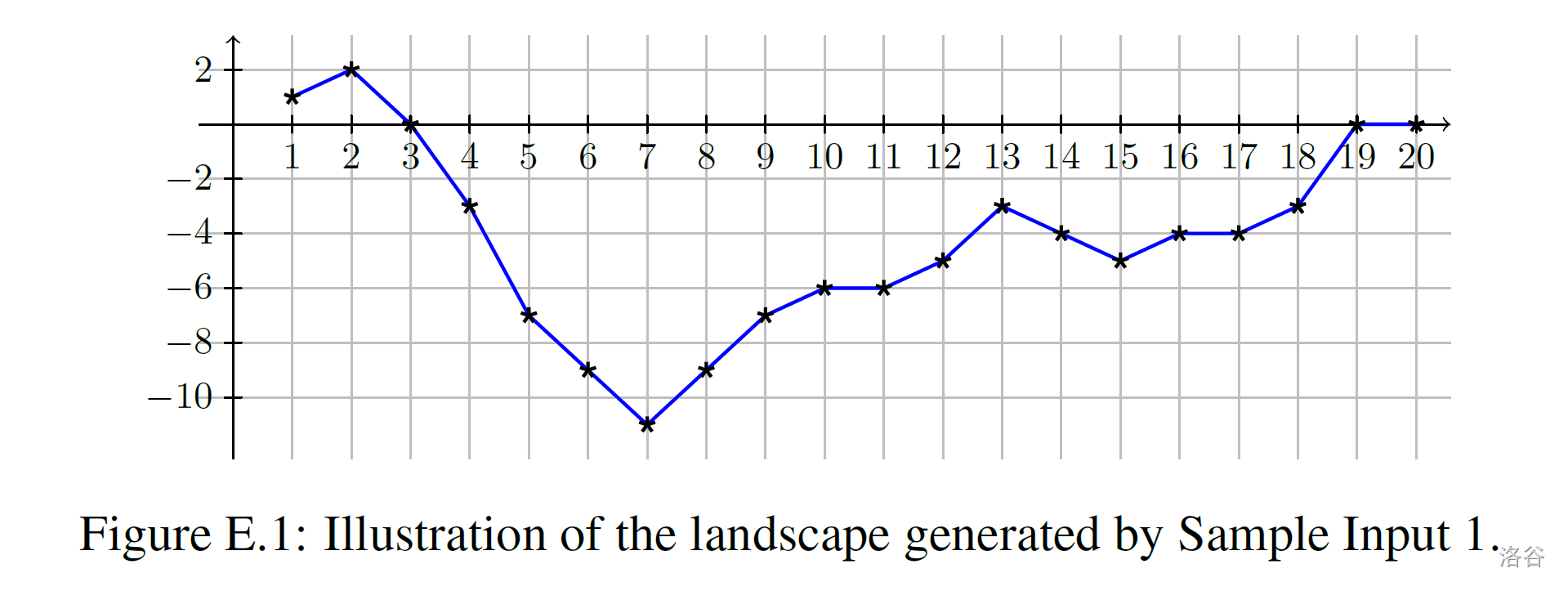
### 题目背景 ICPC2020 WF E Interactive Creative Players Collective (ICPC)正在创作一款游戏，他们想为它生成真实的地形。一位ICPC工程师受地质过程启发，提出了一种算法，该算法从一个平地开始，重复地通过上升或下降一些连续的区块来改变地形，这样就会形成地垒（即上升的区块）和地堑（即下降的区块）。上升或下降的区块是随机选择的。ICPC希望通过这种方法获得真实的地形。 你的任务是根据所有的更改地形指令输出得到的地形，地形可表示为一个由$n$个整数组成的数组，每个整数代表$x$轴上的点$1$到$n$的海拔高度值。图表E.1是将这些值用折线连接起来的一个例子。  最初，这$n$个点的海拔都是0，接下来这个图形会受到一系列的修改，每条修改指令是以下四条之一，并且有两个参数$x_1 \le x_2$ ： - $\texttt{R}$: Raise（上升）——将$x_1$到$x_2$的所有点的海拔均增加$1$。 - $\texttt{D}$: Depress（下降）——将$x_1$到$x_2$的所有点的海拔均减少$1$。 - $\texttt{H}$: Hill（山丘）——在$x_1$到$x_2$之间形成一座“山丘”。 - $\texttt{V}$: Valley（峡谷）——在$x_1$到$x_2$之间形成一条“峡谷”。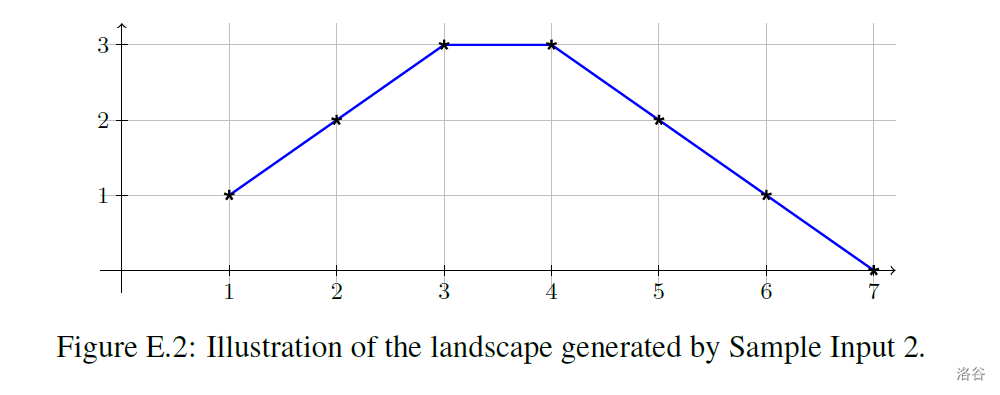 向现有地形添加一座“山丘”的原理如下：点$x_1$和$x_2$的海拔增加1；如果$x_2-x_1>1$，那么点$x_1+1$和$x_2-1$的海拔增加2；如果$x_2-x_1>3$，那么点$x_1+2$和$x_2-2$的海拔增加3；以此类推。图表E.2是一个例子。添加一条“峡谷”与上述原理相同，只是海拔是减少而非增加。海拔改变最大的点在$x_1$和$x_2$的中间，如果$x_2-x_1$是偶数，就会有两个相邻的点海拔改变最大，否则只有一个点。 

输入的第一行包含两个整数$n$和$k$，其中$n$ ($1 \le n \le 2\times10^5$)代表点的数量，$k$ ($0 \le k \le 2\times10^5$)代表修改指令的数量。$x$轴上的$n$个点被编号为$1$到$n$。 接下来的$k$行描述修改。每行包含一个字符$c$和两个整数$x_1$和$x_2$，其中$c$ (为$\texttt{R}$, $\texttt{D}$, $\texttt{H}$, $\texttt{V}$之一)代表操作种类，$x_1$和$x_2$ ($1 \le x_1 \le x_2 \le n$)是具体参数。

输出共$n$行，其中第$i$行为所有修改完成后点$i$的海拔。