P8137 [ICPC 2020 WF] 'S No Problem

ICPC2020 WF J

The Yllihc Engineering and Technological Institute (YETI), located in upper northern Snowblovia, has two problems: snow and money. Specifically, they have too much of the former and not enough of the latter. Every winter (and fall and spring for that matter) the campus is covered with blankets of snow. The maintenance staff must clear all the sidewalks connecting the campus buildings, but they have only two snow blowers and have been told in no uncertain terms that they cannot expect to obtain any more in the near future. To preserve the longevity of these two precious machines, the staff has decided on the following snow removal procedure. Each machine is assigned a fixed route connecting two of the buildings on campus. Whenever snow must be removed, each snow blower is taken from the building at one end of its route and used to clear snow, ending up in the building at the other end of its route, where it is stored until the next snowfall. The reverse movement will occur during the next snow removal event---each machine will trace its assigned route in the opposite direction. This process cycles throughout the eleven-month snow season. Note that a route might involve doubling back over sidewalks that have already been cleared. Also, it is possible that the same building might be an endpoint for both snow blower routes. 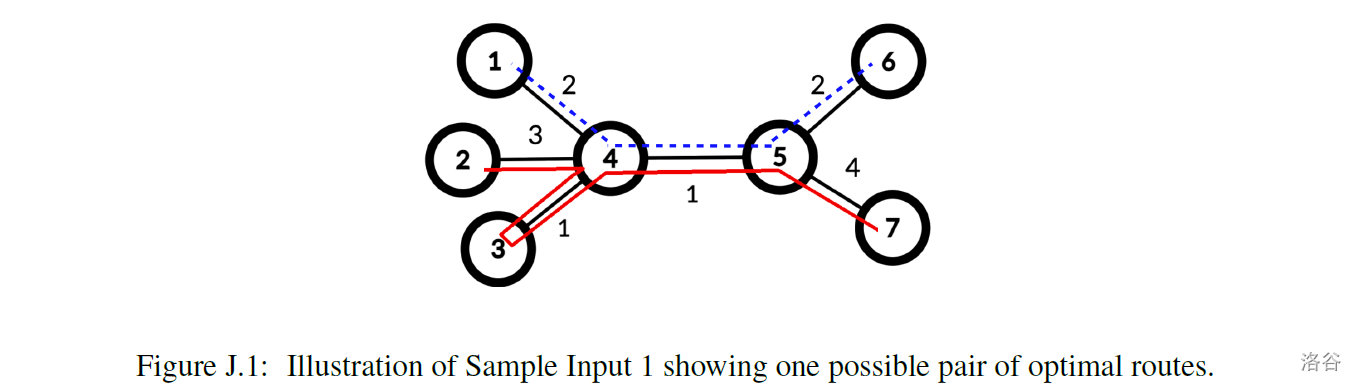The campus sidewalks are laid out in the form of a tree. To run the machines as little as possible, the staff wants to minimize the total distance that the snow blowers must travel as they are guided along their routes. Figure J.1 shows an optimal solution for the sidewalk layout of the first sample input.  The YETI maintenance crew would ask the Computer Science Department at YETI to figure this out, but they were wiped out in the Great Blizzard of '$06$, so they have come to you for help.

The first line of input contains an integer $n$ ($4\leq n\leq 100\,000$), the number of buildings on the YETI campus. Buildings are numbered from $1$ to $n$. Each of the remaining $n-1$ lines contains three integers $a$, $b$, and $d$ indicating that a two-way sidewalk exists between buildings $a$ and $b$ ($1 \leq a, b \leq n$; $a\ne b$) of length $d$ ($1\leq d\leq 500$).

Output the minimum total distance the two machines must travel in any snow removal event.