P8172 [CEOI 2021] L-triominoes
题目背景
译自 CEOI2021 Day1 T2. [L-triominoes](https://hsin.hr/ceoi/competition/ceoi2021_day1_tasks.pdf)。
题目描述
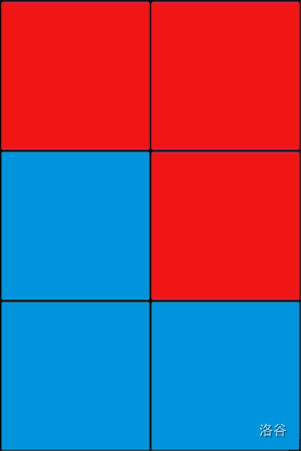
给出一个 $H\times W$ 的矩形,我们称其中 $1\times 1$ 的最小矩形为单元格。这个矩形现在有 $K$ 个单元格遗失了。现在请问能否用形如下图的纸片完全覆盖整个矩形。

我们认为一个矩形能被覆盖,当且仅当其所有未遗失的单元格恰好被纸片覆盖一次且没有纸片超出矩形或覆盖在遗失的单元格上。当然,纸片可以垂直或 $90°$ 旋转。
输入格式
输入的第一行包含三个非负整数,分别是 $W,H,K$,表示矩形的列数,行数和遗失的单元格数量。
接下来 $K$ 行,每行两个正整数 $x_i,y_i$ 表示一个遗失单元格的坐标。保证给出的单元格坐标互不相同。
输出格式
若能刚好覆盖则输出一行一个字符串 `YES`,否则输出一行一个字符串 `NO`。
说明/提示
#### 样例解释
对于样例一,如图是一种合法的覆盖:

对于样例二,你永远无法覆盖 $(1,1)$ 上的单元格。

对于样例三,如图是一种合法的覆盖:
#### 子任务
所有测试点均满足 $1\leq W\leq 13$,$2\leq H\leq 10^9$,$0\leq K\leq 250$,$1\leq x_i\leq W$,$1\leq y_i\leq H$。
| 子任务编号 | 分值 | 约束 |
| :--------: | :--: | :-----------------------------------------: |
| $1$ | $10$ | $2\leq W\leq 13$,$2\leq H\leq 10^3$,$K\leq 250$ |
| $2$ | $7$ | $2\leq W\leq 13$,$2\leq H\leq 10^9$,$K=0$ |
| $3$ | $11$ | $2\leq W\leq3$,$2\leq H\leq 10^9$,$K\leq 250$ |
| $4$ | $17$ | $4\leq W\leq 6$,$2\leq H\leq 10^9$,$K\leq 250$ |
| $5$ | $35$ | $7\leq W\leq 13$,$2\leq H\leq 10^9$,$K\leq 250$ |
| $6$ | $20$ | $2\leq W\leq 13$,$2\leq H\leq 10^9$,$K\leq 250$ |