P8176 [CEOI 2021] Wells

译自 CEOI2021 Day2 T3. [Wells](https://hsin.hr/ceoi/competition/ceoi2021_day2_tasks.pdf)。 **滥用评测资源将被封号。**

给出一个有 $N$ 个结点的树和一个正整数 $K$，确定是否存在一个顶点子集，使得任意恰好包含 $K$ 个顶点的路径都**恰好**有一个来自该子集的顶点。此外，您需要找到模 $10^9+7$ 的此类子集的数量（不存在则为 $0$）。

第一行两个整数 $N$ 和 $K$。 接下来 $N-1$ 行，每行两个整数 $u$ 和 $v$，表示节点 $u$ 和节点 $v$ 之间存在一条无向边。

第一行一个字符串，如果存在输出 `YES`，否则输出 `NO`。 第二行输出一个整数，表示满足条件的子集个数，如果不存在，输出 $0$。

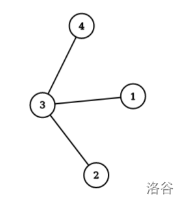
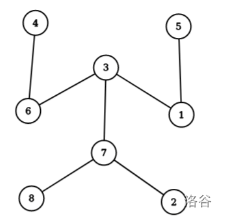
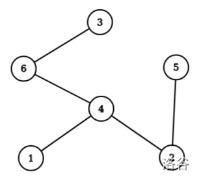
#### 样例解释1  满足条件的子集有：$\{3\}$，$\{1,2,4\}$。 #### 样例解释2  #### 样例解释3  只有一条长度为 $5$ 的路径，该路径包含节点 $3,6,4,2,5$。这些节点中必须恰好有一个在子集中，并且节点 $1$ 是否在子集中没有区别。 因此所有满足条件的子集有：$\{3\}$，$\{1,3\}$，$\{6\}$，$\{1,6\}$，$\{4\}$，$\{1,4\}$，$\{2\}$，$\{1,2\}$，$\{5\}$，$\{1,5\}$。 #### 数据范围与约定 对于 $100\%$ 的数据：$2\leq K\leq N\le 1.5\times 10^6$。 | 子任务 | 分值 | 约束 | | :----: | :--: | :---------------------------------------------------: | | $1$ | $30$ | $2\leq K\leq N\le 200$ | | $2$ | $20$ | $2\leq K\leq N\le 10^4$ | | $3$ | $20$ | $2\leq K\leq N\le 5\times 10^5$ | | $4$ | $30$| $2\leq K\leq N\le 1.5\times 10^6$ |