P8192 [USACO22FEB] Paint by Rectangles P
题目背景
翻译来自 @wlzhouzhuan。
题目描述
在她之前的作品受到好评后,Bessie 得到了一份设计绘画套装的工作。她通过在平面中选择 $N\ (1\le N\le 10^5)$ 个平行于坐标轴的矩形来设计该画作,没有两条边是共线的。这些矩形的边界定义了绘画着色区域的边界。
作为一名先锋艺术家,Bessie 觉得这幅画应该像一头荷斯坦奶牛。更具体地,由矩形构成的每个区域都被着色为黑色或白色,没有两个相邻区域具有相同的颜色,并且所有矩形之外的区域都被着色为白色。
选完矩形后,Bessie 想根据参数 $T$ 让你输出:
- 若 $T=1$,则输出区域总数;
- 若 $T=2$,则依次输出白色区域数量和黑色区域数量。
**注意:本题的时间限制为 4s,是默认的 2 倍。**
输入格式
第一行,输入 $N$ 和 $T$。
接下来 $N$ 行,每行读入 $x_1,y_1,x_2,y_2$,表示一个左下角为 $(x_1,y_1)$,右上角为 $(x_2,y_2)$ 的矩形。
数据保证 $x_i$ 形成了一个 $1\sim 2N$ 的排列,$y_i$ 同理。
输出格式
若 $T=1$,输出一个整数;否则输出两个整数,用空格隔开。
说明/提示
**【样例解释 #1】**
有 $2$ 个白色区域和 $2$ 个黑色区域,共有 $4$ 个区域。所有矩形的边界连通,因此该输入满足 subtask 3。

**【样例解释 #2】**
右上方的矩形不与其余的矩形连通,因此该输入不满足 subtask 4。
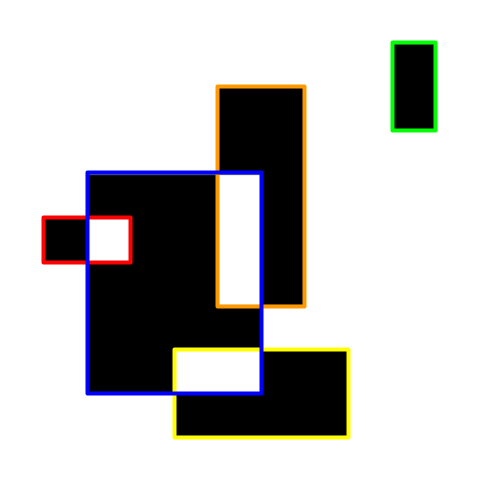
**【数据范围】**
- subtask 1:数据 $3\sim 4$ 满足 $N\le 10^3$;
- subtask 2:数据 $5\sim 7$ 满足不存在两个矩形相交;
- subtask 3:数据 $8\sim 10$ 满足 $T=1$,且所有矩形的边界连通;
- subtask 4:数据 $11\sim 13$ 满足 $T=2$,且所有矩形的边界连通;
- subtask 5:数据 $14\sim 18$ 满足 $T=1$;
- subtask 6:数据 $19\sim 23$ 满足 $T=2$。