P8354 [SDOI/SXOI2022] 多边形

给定一个正 $n$ 边形，除了这个正 $n$ 边形的 $n$ 个顶点，顺时针第 $i$ 条边上还有额外的 $a_i-1$ 个顶点等分这条线段，也就是说，第 $i$ 条边被顶点分成了长度相等的 $a_i$ 段。 你可以在顶点之间连接一些线段，但是连接完线段之后，图中的任意两条新添加的线段只能在端点处有交，此外，新的线段也不应该与多边形的边有所重合。 我们称添加了若干线段之后得到的图为一个三角剖分，当且仅当多边形内的每个面都是一个三角形，注意，三角形的边上可以有原来凸多边形边上的顶点。 给定这样一个凸多边形，其有多少种满足上述条件的三角剖分? 你只需要计算方案数模 $998244353$ 的答案就行。

第一行输入一个正整数 $n$，表示凸多边形的边数。 第二行输入 $n$ 个正整数，其中第 $i$ 个正整数为 $a_i$，含义如题目描述中所示。

输出一行一个整数，表示满足题目要求的三角剖分的方案数模 $998244353$ 的结果。

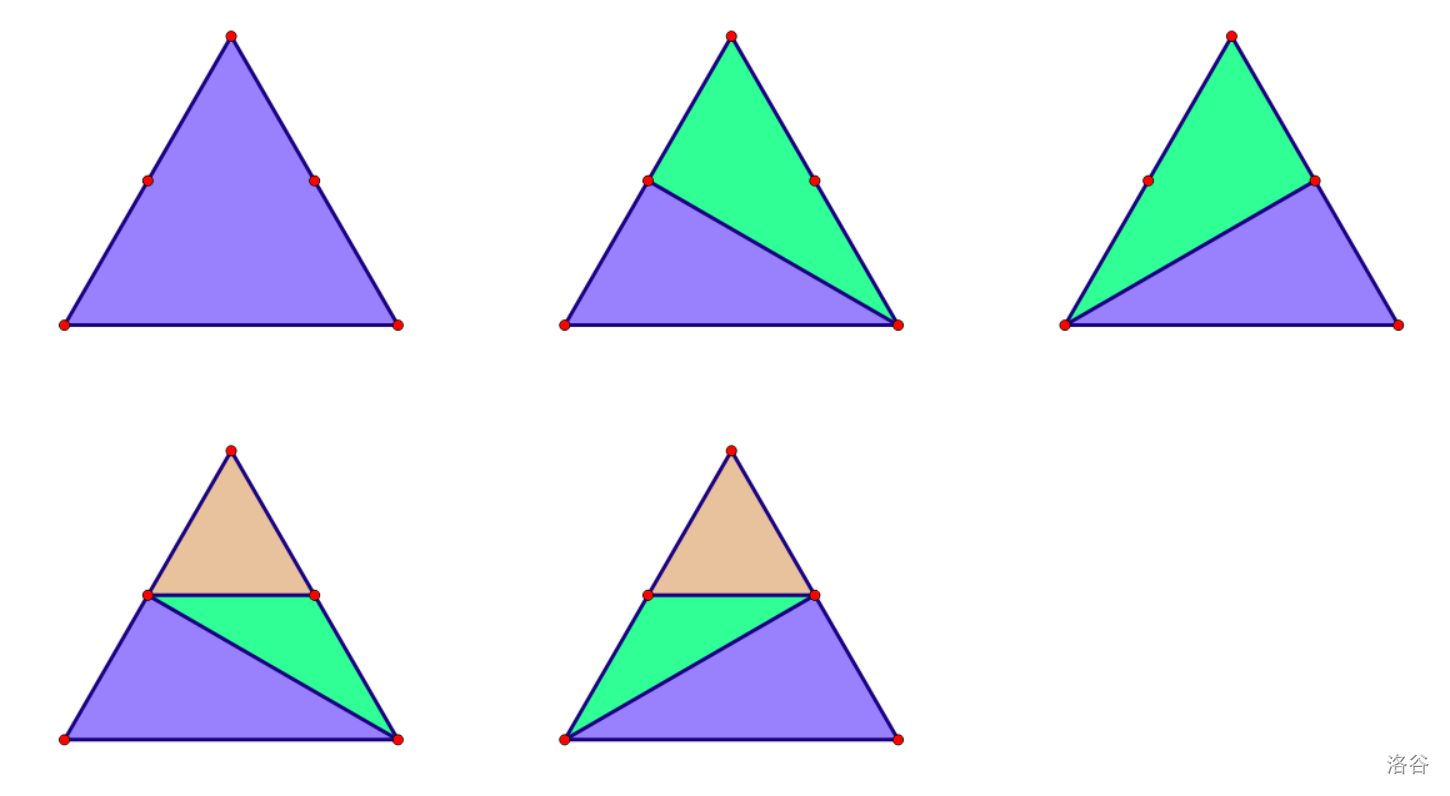
**【样例 1 解释】** 5 种方案如图所示。  **【数据范围】** 对于 $10 \%$ 的数据，保证 $\sum a_{i} \leq 300$。 对于 $50 \%$ 的数据，保证 $\sum a_{i} \leq 5000$。 对于 $100 \%$ 的数据，保证 $n \geq 3$，$a_{i} \geq 1$， $\sum a_{i} \leq 5 \times 10^{5}$。 注：本题无大样例下载