P8389 [COI 2021] Izvanzemaljci
题目描述
**译自 [COI 2021](https://hsin.hr/coci/archive/2020_2021/) T3「[Izvanzemaljci](https://hsin.hr/coci/archive/2020_2021/olympiad_tasks.pdf)」**
在二维平面上有 $N$ 个整点 $(x_i,y_i)$,请找出 $K$ 个不相交的正方形,使得所有整点在正方形内或在正方形上,如有多解,求出在所有构造方案中面积最大的正方形面积最小的那一种,如果还有多解,输出任意一组即可。
两个正方形如果没有边相交或相碰,并且没有一个正方形完全被另一个正方形包含的情况,则这两个正方形不相交。
输入格式
第一行为两个整数 $N$,$K$。
接下来 $N$ 行,一行两个整数 $x_i$,$y_i$。
输出格式
共 $K$ 行,每行三个整数 $a_i$,$b_i$,$l_i$,表示有一个左下角为 $(a_i,b_i)$,边长为 $l_i$ 的正方形。
您需要保证 $0\le |a_i|,|b_i|\le 3\times 10^9$,$1\le l_i\le 2\times 10^9$。
说明/提示
【样例解释】
样例 #2 解释:

样例 #3 解释:
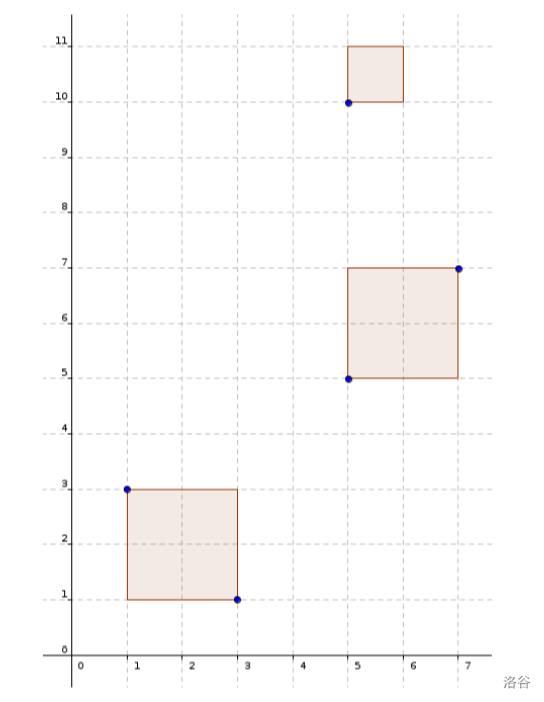
【数据范围】
对于全部数据,有 $1\le N\le 10^5$,$1\le K\le 3$,$0\le |x_i|,|y_i|\le 10^9$。
| Subtask | 限制 | 分数 |
| :-----: | :----------------: | :--: |
| $1$ | $K=1$ | $5$ |
| $2$ | $K=2$ | $21$ |
| $3$ | $N\le 12$,$K=3$ | $12$ |
| $4$ | $N\le 10^3$,$K=3$ | $30$ |
| $5$ | $K=3$ | $32$ |