P8439 Altale (Fan-made FTR 7)
题目背景
[](https://music.163.com/#/program?id=2067229684)
为什么评级 7?
Powerless:Equilibrium FTR 9.
题目描述
小机器人又在钓星星了。
星星在天空中形成了若干个星座,每个星座有一个“中心点”,如果星星脱离了与中心点的直接或间接的联系,那么星星就会从星座中脱离,掉落到地面上。
经过小机器人日日夜夜的观测,他发现了这些星座的性质:每一个星座内部都是联通的,星星的联系的数量总与星座中星星的数量相等。
另外,不同的星座之间星星没有联系,同一个星座中的星星都有间接或直接的联系。
他通过观测天体运动给星星编了号,他发现每个星座的中心点都是星座中编号最小的星星。
可惜的是,小机器人只能通过随(diao)缘(yu)的方式获得取消这些联系的钥匙。
小机器人非常贪心,想要用尽量少的时间获得尽量多的星星。
他想要 $k$ 颗星星,你能告诉他他至少需要钓上几把钥匙吗?
如果你解决了这个问题,说不定小机器人会送给你几颗星星哦~
**[简化题意](https://www.luogu.com.cn/paste/5nhqqjzm)**
输入格式
第一行两个整数 $n,k$,表示**天空中**所有的星星的**总数**和星星之间联系**总数**,和小机器人希望获得的星星数。
接下来 $n$ 行,每行两个整数 $u,v$ 表示 第 $u$ 颗和第 $v$ 颗星星之间存在联系。
保证任意星座内星星联系条数等于星星数,星星不会有自己到自己的联系,不会有两条联系建立在同样两颗星星上。
输出格式
一行一个整数,表示小机器人需要获得足够的星星所需最少的钥匙数。
说明/提示
**本题采用捆绑测试。**
设星座共有 $l$ 个。
对于 $100\%$ 的数据,保证 $1\le n\le 10^6,1\le k\le n-l$。
Subtask 1:对于 $20\%$ 的数据,保证 $n\le 1000$。
Subtask 2:对于 $10\%$ 的数据,保证 $l\le 5$。
Subtask 3:对于 $20\%$ 的数据,保证 $l\le 15$。
Subtask 4:无特殊限制。
----
样例解释 $1$:
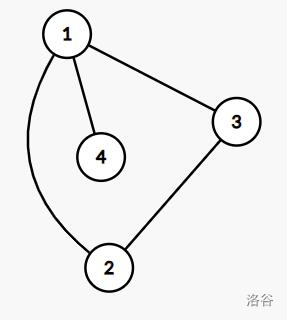
消除 $(1,4)$ 间联系即可。
样例解释 $2$:
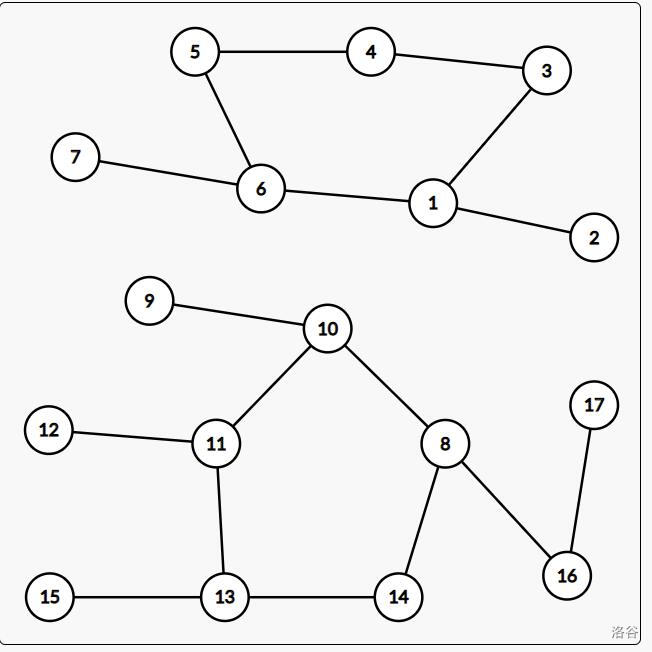
消除 $(8,14),(8,10),(8,16)$ 三条联系即可。
可以证明没有消除联系更少的方法。
可能有别的方法也仅需要消除 $3$ 条联系。