P8488 「Wdoi-(-1)」恋弹者们的黑集市

> 天弓千亦有言：「能力卡终将大势所趋归于陈腐，集市终将回归日常，这是发展规律。」但不知为何和神明所说相悖，卡片的价值遭到了炒作。有人在炒作卡的价值吗废话？又或者说，有倒爷在囤积这些卡片吗？卡片市场秩序完全陷入混乱之时，即便是神明也无法介入的集市，就此出现。 $$\quad\tag*{\small\textit{---TH18.5 恋弹者们的黑集市}}$$ 魔理沙正在调查妖怪之山的高地，来收集逸散在各地的能力卡片。就在此时，她遇到了住在此处的驹草山如。 在河童与天狗间游刃有余的驹草山如，掌握着此地大量的资源。显而易见的，她掌握着大量的能力卡片——这正是魔理沙探访的目标。 「想要这些卡片吗，那就让我们玩一个游戏吧」 「赢了，这些卡片就都归你；输了，你可要交出身上所有的卡片。」

### 原始题意 驹草山如将一个六面写满权值的骰子放在了棋盘上。棋盘上花花绿绿写着很多数字。第 $i$ 行第 $j$ 列写有数字 $a_{i-1,j-1}$。 「你能否获得这些能力卡片，取决于你获得的分数。」 魔理沙有两种方法移动这个骰子：将骰子向下一列**翻转**，或者向下一行**翻转**。值得注意的是，翻转骰子后，骰子每面上的数字就会随着翻滚而改变。现在魔理沙需要将骰子滚动至第 $n$ 行第 $m$ 列。 魔理沙的分数被定义为，所有时刻，骰子与棋盘上的数字接触的那一面的数字，乘上棋盘上该数字，再累加起来的和。只有魔理沙最大化这个和，她才能获取她所需要的卡片。 你能帮帮魔理沙吗？ ### 简要题意 有一个 $n\times m$ 大小的棋盘，第 $i$ 行第 $j$ 列写有数字 $a_{i-1,j-1}$。 现在有一个骰子，六个面按照前、后、左、右、上、下的顺序，依次写有数字 $w_0,w_1,w_2,w_3,w_4,w_5$。现在骰子摆放在 $(0,0)$ 位置，需要将它**滚动**至 $(n-1,m-1)$。  骰子只有两种方式滚动：向下一行翻滚、向下一列翻滚。我们记一种方案的权值为，整个过程中（包括骰子在起点和终点时），骰子**最底面**上写着的数字，与此时骰子所在格子上写着的数字的乘积之和。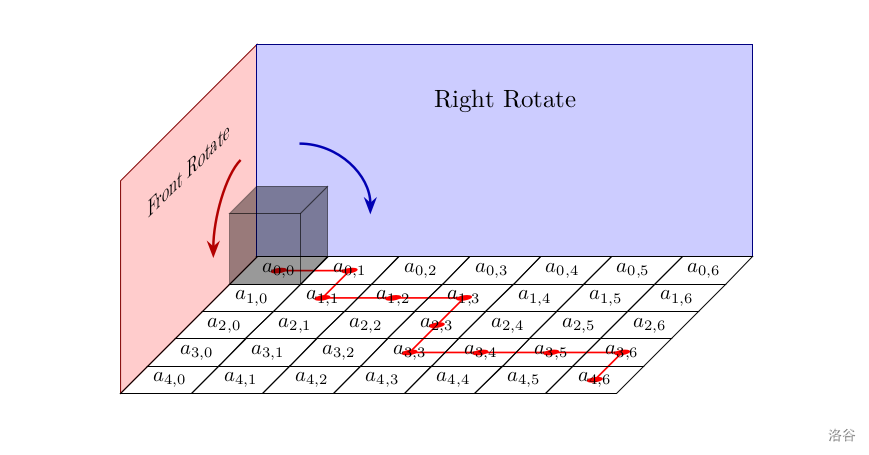  （为了方便读者阅读，骰子上的数字已经隐去） 现在你需要最大化这个乘积之和。

- 第一行有两个正整数 $n, m$，表示棋盘的大小。 - 接下来 $n$ 行 $m$ 列描述棋盘内元素的值 $a_{i,j}$。 - 接下来一行有六个整数，分别表示 $w_0,w_1,w_2,w_3,w_4,w_5$。

- 输出共一行一个整数，表示可以获得的最大权值。

### 样例解释 #### 样例 1 解释 一种最优的方案为，$(0,0)\to(0,1)\to(1,1)\to(1,2)\to(1,3)\to(2,3)\to(3,3)\to(3,4)\to(4,4)$。 总权值为 $2+8+19+19+3+8+8+17+13=97$。 #### 样例 2 解释 一种最优的方案为，$(0,0)\to(0,1)\to(1,1)\to(1,2)\to(1,3)\to(1,4)$。 ### 数据范围及约定 $$ \def\arraystretch{1.5} \begin{array}{|c|c|c|c|}\hline \textbf{Subtask} & \bm{n,m\le} & \textbf{特殊性质} & \textbf{分值} \\\hline 1 & 10 & - & 10 \\\hline 2 & 100 & - & 30 \\\hline 3 & 10^3 & \textbf{A} & 10 \\\hline 4 & 10^3 & - & 50 \\\hline \end{array}$$ - **特殊性质** $\textbf{A}$：保证 $w_i=1,i=0,1,2,\cdots 5$。 对于全部数据，保证 $1\le n,m\le 10^3$，$|a_i|\le 10^3$，$|w_i|\le 10^3$。