P8492 [IOI 2022] 无线电信号塔
题目背景
### 由于技术限制,请不要使用 C++ 14 (GCC 9) 提交本题。
这是一道交互题,你只需要实现代码中要求的函数。
你的代码不需要引用任何额外的头文件,也不需要实现 main 函数。
题目描述
雅加达有 $N$ 个无线电信号塔。这些信号塔排布成一条直线,并且从左到右依次编号为从 $0$ 到 $N - 1$。
对于每个满足 $0 \le i \le N - 1$ 的 $i$,信号塔 $i$ 的高度为 $H_i$ 米。
所有塔的高度都是**不同的**。
对于某个为正数的信号干扰参数 $\delta$,一对信号塔 $i$ 和 $j$ ($0 \le i \lt j \le N - 1$) 之间能够互相通信,当且仅当存在一个中间信号塔 $k$ 满足如下条件:
* 塔 $i$ 在塔 $k$ 的左边,并且塔 $j$ 在塔 $k$ 的右边,即 $i \lt k \lt j$;
* 塔 $i$ 和塔 $j$ 的高度都至多为 $H[k] - \delta$ 米。
Pak Dengklek 想租一些信号塔来组建他的新无线电网络。
你的任务是回答 Pak Dengklek 提出的 $Q$ 个询问。这些询问的形式如下:
给定参数 $L, R$ 和 $D$ ($0 \le L \le R \le N - 1$ 且 $D > 0$),在满足下述所有条件时,Pak Dengklek 最多能够租多少个信号塔:
* Pak Dengklek 只能租编号在 $L$ 和 $R$ 之间的信号塔(包括 $L$和 $R$);
* 信号干扰参数 $\delta$ 的值为 $D$;
* Pak Dengklek 租的信号塔两两之间必须能够进行通信。
注意,无论中间信号塔 $k$ 是否被租,两个已租的信号塔都可以借助信号塔 $k$ 进行通信。
输入格式
你需要实现以下函数:
```go
void init(int N, int[] H)
```
* $N$: 信号塔的数量。
* $H$: 一个长度为 $N$ 的数组,给出信号塔的高度。
* 这个函数恰好被调用一次,且在函数 `max_towers` 的所有调用之前。
```go
int max_towers(int L, int R, int D)
```
* $L$, $R$:信号塔编号区间的边界。
* $D$:信号干扰参数 $\delta$ 的值。
* 该函数应返回 Pak Dengklek 最多能租的信号塔数量(用于组建信号网络),这里 Pak Dengklek 只能租 $L$ 和 $R$之间(包含 $L$ 和 $R$)的信号塔,且信号干扰参数 $\delta$ 的值是 $D$。
* 该函数将被调用恰好 $Q$ 次。
输出格式
考虑如下函数调⽤序列:
```go
init(7, [10, 20, 60, 40, 50, 30, 70])
```
```go
max_towers(1, 5, 10)
```
Pak Dengklek 可以租编号为 $1$, $3$ 和 $5$ 的信号塔。
下面给出了这个例子的示意图,其中的灰色梯形表示被租的信号塔。
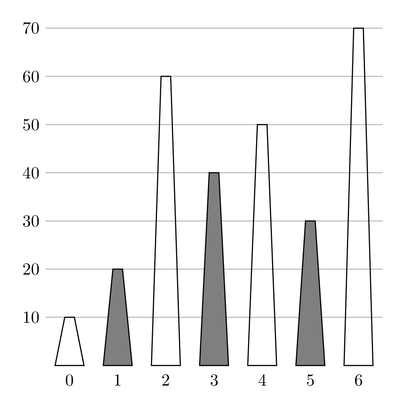
信号塔 $3$ 和 $5$ 可以借助信号塔 $4$ 进行通信,这是因为 $40 \le 50 - 10$ 且 $30 \le 50 - 10$。
信号塔 $1$ 和 $3$ 可以借助信号塔 $2$ 进行通信。
信号塔 $1$ 和 $5$ 可以借助信号塔 $3$ 进行通信。
无法租超过 $3$ 个信号塔,因此函数应返回 $3$。
```go
max_towers(2, 2, 100)
```
在这个区间里只有 $1$ 个信号塔,所以 Pak Dengklek 只能租借 $1$ 个信号塔。
因此函数应返回 $1$。
```go
max_towers(0, 6, 17)
```
Pak Dengklek 可以租信号塔$1$ 和 $3$ 。
信号塔 $1$ 和 $3$ 可以借助信号塔 $2$进行通信,这是因为 $20 \le 60 - 17$ 且 $40 \le 60 - 17$。
无法租赁超过 $2$ 个信号塔,因此函数应返回 $2$。
说明/提示
### 约束条件
* $1 \le N \le 100\;000$
* $1 \le Q \le 100\;000$
* $1 \le H_i \le 10^9$ (对于所有满足 $0 \le i \le N - 1$ 的 $i$ )
* $H_i \ne H_j$ (对于所有满足 $0 \le i \lt j \le N - 1$ 的 $i$ 和 $j$ )
* $0 \le L \le R \le N - 1$
* $1 \le D \le 10^9$
### 子任务
1. (4 分) 存在一个满足下述所有条件的信号塔 $k$ ($0 \le k \le N - 1$)
* 对于 $0 \le i \le k - 1$ 的每个 $i$:$H_i \lt H_{i + 1}$
* 对于 $k \le i \le N - 2$ 的每个 $i$:$H_i \gt H_{i + 1}$
2. (11 分) $Q = 1$,$N \le 2000$
3. (12 分) $Q = 1$
4. (14 分) $D = 1$
5. (17 分) $L = 0$,$R = N - 1$
6. (19 分) $D$ 的值在 `max_towers` 的所有调用中都是相同的
7. (23 分) 没有额外的限制
### 评测程序示例
评测程序示例读取如下格式的输入:
* 第 $1$ 行:$N \; Q$
* 第 $2$ 行:$H_{0} \; H_{1} \; \ldots \; H_{N - 1}$
* 第 $3 + j$ 行($0 \le j \le Q - 1$):$L \; R \; D$(对应第 $j$ 次询问)
评测程序示例按照如下的格式打印你的答案:
* 第 $1 + j$ 行($0 \le j \le Q - 1$):`max_towers` 对第 $j$ 次询问的返回值
### 约定
题面在给出函数接口时,会使用一般性的类型名称 `void`、`int`、`int64`、`int[]`(数组)和 `int[][]`(数组的数组)。
在 C++ 中,评测程序会采用适当的数据类型或实现,如下表所示:
| `void ` | `int` | `int64` | `int[]` |
| ------- | ----- | ----------- | ------------------ |
| `void ` | `int` | `long long` | `std::vector` |
| `int[][]` | 数组 `a` 的长度 |
| ------------------------------- | ------------------- |
| `std::vector` | `a.size()` |