P8495 [IOI 2022] 千岛
题目背景
不要 $\texttt{\#include "islands.h"}$。
题目描述
千岛是爪哇海里一组美丽的岛屿,其中有 $N$ 个岛屿,编号为从 $0$ 到 $N - 1$。
有 $M$ 艘独木舟在岛屿之间航行,编号为从 $0$ 到 $M - 1$。对于满足 $0 \le i \le M - 1$ 的所有 $i$,独木舟 $i$ 可以停靠在岛屿 $U_i$ 或 $V_i$,并且在岛屿 $U_i$ 和 $V_i$ 之间航行。具体来说,当独木舟停靠在岛屿 $U_i$ 时,可以用它从岛屿 $U_i$ 去往岛屿 $V_i$,此后该独木舟就变成停靠在岛屿 $V[i]$。类似地,当该独木舟停靠在岛屿 $V[i]$ 时,它可以从岛屿 $V_i$ 航向岛屿 $U_i$,此后该独木舟就变成停靠在岛屿 $U_i$。在初始时,该独木舟停靠在岛屿 $U_i$。可能有多艘独木舟能用于在同一对岛屿之间航行。也可能会有多艘独木舟停靠在同一个岛屿处。
出于安全考虑,各艘独木舟在每次航行后必须进行维修,因此同一独木舟不允许紧接着完成两次航行。也就是说,在用完某艘独木舟 $i$ 后,必须先用过另外某艘独木舟,才能再启用独木舟 $i$。
Bu Dengklek 想策划一次在部分岛屿之间的旅行。她的旅程是**合理的**,当且仅当满足如下条件:
- 她的旅程应从岛屿 $0$ 开始,并且在该岛屿结束。
- 她应该游览岛屿 $0$ 之外的至少一个岛屿。
- 在旅行结束后,每艘独木舟应停靠在旅行开始前它所在的岛屿。也就是说,对于满足 $0 \le i \le M - 1$ 的所有 $i$,独木舟必须停靠在岛屿 $U_i$。
请你帮助 Bu Dengklek 找出包括至多航行 $2\;000\;000$ 次的合理旅行,或者告诉她不存在合理旅行。
可以证明,在本题所给出的约束条件下(参见约束条件部分),如果存在合理旅行,则必然存在航行次数不超过 $2\;000\;000$ 次的合理旅行。
输入格式
你要实现如下函数:
```go
union(bool, int[]) find_journey(int N, int M, int[] U, int[] V)
```
- $N$:岛屿数量。
- $M$:独木舟数量。
- $U$, $V$:长度为 $M$ 的两个数组,给出独木舟航行的岛屿。
- 该函数应当返回一个布尔类型或者整数数组。
- 如果不存在合理旅程,该函数应返回 `false`。
- 如果存在合理旅程,你有两个选择:
- 如果想得到全部的分数,该函数应返回一个至多包含 $2\;000\;000$ 个整数的数组,该数组用来刻画一个合理旅程。更确切地说,该数组中的元素应为旅程中所用独木舟的编号(按照独木舟的使用顺序)。
- 如果想得到部分分数,该函数应返回 `true`,或返回一个包含超过 $2\;000\;000$ 个整数的数组,或返回了一个未给出合理旅程的整数数组(更多细节参见“子任务”部分)。
- 该函数将被调用恰好一次。
输出格式
### 例子 1
考虑如下调用:
```go
find_journey(4, 5, [0, 1, 2, 0, 3], [1, 2, 3, 3, 1])
```
下图给出了岛屿和独木舟。
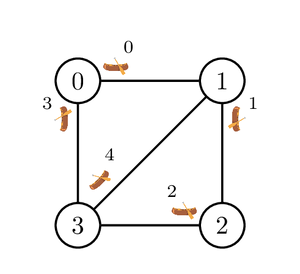
一个可行的合理旅行如下。Bu Dengklek 先依次使用独木舟 $0$,$1$,$2$ 和 $4$。结果是她将在岛屿 $1$ 上。其后,Bu Dengklek 可以再次使用独木舟 $0$,因为该独木舟正停靠在岛屿 $1$,而且她用的上一艘独木舟不是 $0$。再次使用独木舟 $0$ 后,现在 Bu Dengklek 在岛屿 $0$ 上。然而,独木舟 $1$,$2$ 和 $4$ 没有停靠在旅程开始前它们所在的岛屿。接下来 Bu Dengklek 继续她的旅程,使用独木舟 $3$,$2$,$1$,$4$ 和再一次使用 $3$。Bu Dengklek 回到了岛屿 $0$ 上,并且所有独木舟都停靠在旅行开始前它们所在的岛屿。
因此,返回结果 $[0, 1, 2, 4, 0, 3, 2, 1, 4, 3]$ 刻画了一个合理旅程。
### 例子 2
考虑如下调用:
```go
find_journey(2, 3, [0, 1, 1], [1, 0, 0])
```
下图给出了岛屿和独木舟。
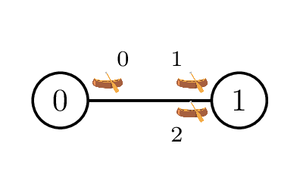
Bu Dengklek 仅能从使用独木舟 $0$ 开始,此后她可以使用独木舟 $1$ 或者 $2$。注意,她不能连续使用独木舟 $0$ 两次。在两种情况下,Bu Dengklek 都回到了岛屿 $0$ 上。然而,有独木舟没停靠在旅行开始前它们所在的岛屿,而 Bu Dengklek 此后却无法再使用任何独木舟,因为唯一停靠在岛屿 $0$ 的独木舟是她刚用过的那艘。由于不存在合理旅程,该函数应当返回 `false`。
说明/提示
### 约束条件
- $2 \le N \le 10^5$;
- $1 \le M \le 2 \times 10^5$;
- $0 \le U_i \le N - 1$ 且 $0 \le V_i \le N - 1$(对于所有满足 $0 \le i \le M - 1$ 的 $i$);
- $U_i \neq V_i$(对于所有满足 $0 \le i \le M - 1$ 的 $i$)。
### 子任务
1. (5 分)$N = 2$。
1. (5 分) $N \le 400$。
对于每一对不同的岛屿 $x$ 和 $y$($0 \le x \lt y \le N - 1$),恰好有两艘可在它们之间航行的独木舟。
其中一艘停靠在岛屿 $x$,而另一艘停靠在岛屿 $y$。
1. (21 分) $N \le 1000$,$M$ 是偶数,而且对于满足 $0 \le i \le M - 1$ 的所有**偶数** $i$,独木舟 $i$ 和 $i + 1$ 都可以用于在岛屿 $U_i$ 和 $V_i$ 之间航行。独木舟 $i$ 最初停靠在岛屿 $U_i$ 处,而独木舟 $i + 1$ 最初停靠在岛屿 $V_i$ 处。形式化地,$U_i = V_{i + 1}$ 且 $V_i = U_{i + 1}$。
1. (24 分) $N \le 1000$,$M$ 是偶数,而且对于满足 $0 \le i \le M - 1$ 的所有**偶数** $i$,独木舟 $i$ 和 $i + 1$ 都可以用于在岛屿 $U_i$ 和 $V_i$ 之间航行。两艘独木舟最初都停靠在岛屿 $U_i$ 处。
形式化地,$U_i = U_{i + 1}$ 且 $V_i = V_{i + 1}$。
1. (45 分)没有额外的约束条件。
对于每个存在合理旅程的测试用例,你的解答:
- 如果返回一个合理旅程,将得到全部分数,
- 如果返回 `true`,或返回一个超过 $2\;000\;000$ 个整数的数组,或返回一个未给出合理旅程的数组,将得到 $35\%$ 的分数,
- 在其他情况下得分为 $0$。
对于每个不存在合理旅程的测试用例,你的解答:
- 如果返回 `false`,将得到全部分数,
- 在其他情况下得分为 $0$。
注意,每个子任务上的最终得分,为该子任务中所有测试用例上的最低得分。
### 评测程序示例
评测程序示例读取如下格式的输入:
- 第 $1$ 行:$N \; M$;
- 第 $2 + i$ 行($0 \le i \le M - 1$):$U_i \; V_i$。
测试程序示例将按照如下格式打印你的答案:
- 如果 `find_journey` 返回一个 `bool`:
- 第 $1$ 行:$0$;
- 第 $2$ 行:如果 `find_journey` 返回 `false` 则为 $0$,否则为 $1$。
- 如果 `find_journey` 返回一个 `int[]`,该数组中的元素记为 $c[0], c[1], \ldots c[k-1]$。测试程序示例打印出:
- 第 $1$ 行:$1$;
- 第 $2$ 行:$k$;
- 第 $3$ 行:$c[0] \; c[1] \; \ldots \; c[k-1]$。
### 约定
题面在给出函数接口时,会使用一般性的类型名称 `void`、`bool`、`int`、`int[]`(数组)和 `union(bool, int[])`。
在 C++ 中,评测程序会采用适当的数据类型或实现,如下表所示:
| `void ` | `bool` | `int` | `int[]` |
| ------- | ------ | ------| ------------------ |
| `void ` | `bool` | `int` | `std::vector` |
| `union(bool, int[])` | 数组 `a` 的长度 |
| -------------------------------------- | ------------------- |
| `std::variant` | `a.size()` |
C++ 语言里,`std::variant` 定义在 `` 头文件中。
一个返回类型为 `std::variant` 的函数可以返回一个 `bool` 或一个 `std::vector`。
以下示例代码给出了三个返回 `std::variant` 的函数,它们都能正常工作:
```cpp
std::variant foo(int N) {
return N % 2 == 0;
}
std::variant goo(int N) {
return std::vector(N, 0);
}
std::variant hoo(int N) {
if (N % 2 == 0) {
return false;
}
return std::vector(N, 0);
}
```