「CGOI-2」No mind to think

“我的王，这个孩子……不纯粹……他……” “嗯。容器不能拥有与人交流的能力，否则可能会在交流中产生思维。它们只应该有猎杀的本能，和战斗的天分。就像我的守卫们一样。” “那些不过是傀儡……” “傀儡也比这个有思维的家伙好。改天把它带走，它真的好吵……我累了，我出去走走。” ~~无敌的勇敢的性感的神秘的迷人的神气的勤勉的强势的华丽的激情的可怕的漂亮的强大的灰色王子左特骂骂咧咧地滚出了白色宫殿。~~

圣巢有 $n$ 个鹿角虫车站和 $n$ 条轨道，第 $i$ 条轨道连接 $u_i$ 和 $v_i$ 两个车站。初始时轨道是单向的，第一次经过第 $i$ 条轨道时，只能从 $u_i$ 到达 $v_i$；第一次经过后该轨道变为双向，既可以从 $u_i$ 到 $v_i$，又可以从 $v_i$ 到 $u_i$。 现在白王在 $1$ 号车站，他要经过若干条轨道到达 $2$ 号车站，再从 $2$ 号车站经过若干条轨道到达 $3$ 号车站……一直到 $x$ 号车站。因为白王需要尽快走遍整个王国以便探清瘟疫的情况，所以他问你，当 $x$ 取遍 $[2,n]$ 中的每一个整数时，所经过的最少的轨道数分别是多少。

第一行一个整数 $n$，表示车站数与轨道数。 接下来 $n$ 行，每行两个整数。第 $i$ 行的数 $u_i,v_i$ 表示第 $i$ 条轨道第一次经过时只能从 $u_i$ 走到 $v_i$，此后可以双向经过。

输出 $n-1$ 行，每行一个数，第 $i$ 个数表示当 $x=i+1$ 时，经过的最少轨道数。

7
1 7
7 6
1 2
2 3
3 4
4 5
5 6

1
2
3
4
5
10

6
1 4
4 2
2 6
6 1
6 3
1 5

2
4
7
9
11

18
14 15
8 12
5 4
10 14
15 17
7 5
3 9
9 18
11 13
1 2
16 10
5 11
5 6
6 8
2 3
2 7
18 16
7 10

1
2
6
7
8
10
13
19
22
26
30
35
40
41
45
49
54

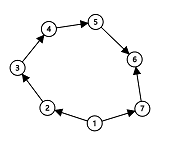
### 样例说明 对于样例 1，地图如下所示：  $x=2,3,4,5,6$ 的最短路径均为沿着 $1\to 2\to3\to4\to5\to6$ 这条路径走，答案分别是 $1,2,3,4,5$。 $x=7$ 时，若仍按照上述路径走，就不能从 $6$ 号车站直接通过 $7\to 6$ 这条轨道到 $7$ 号车站，因为这条轨道还是单向的。绕路回去需要再经过 $6$ 条轨道，总共 $11$ 条轨道。 但如果先走一遍 $7\to6$，即沿着 $1\to7\to6\to7\to1\to2\to3\to4\to5\to6$ 的路径走，来到 $6$ 时就能直接走到 $7$，总共只需要经过 $10$ 条轨道，同时也满足了依次经过 $1\sim 7$ 号点，比上一种方案更优。 --- ### 数据范围 **本题采用捆绑测试。** | 编号 | $n$ |分值| | :-: | :-: | :-: | | 0 | $\le6$ | 10pts| | 1 | $\le18$ | 20pts | | 2 | $\le3\times10^3$ | 32pts | | 3 | $\le5\times10^5$ | 38pts | 对于 $100\%$ 的数据，$3\le n\le5\times10^5$。 数据保证从 $1$ 号车站出发可以到达任意车站，且无重边自环、二元环。