P8520 [IOI 2021] 喷泉公园
题目背景
### 由于技术限制,请不要使用 C++ 14 (GCC 9) 提交本题。
这是一道交互题,你只需要实现代码中要求的函数。
你的代码不需要引用任何额外的头文件,也不需要实现 `main` 函数。但是你的代码需要声明 `void build(std::vector u, std::vector v, std::vector a, std::vector b)` 函数。
具体的,以下是一种模板:
```cpp
#include
void build(std::vector u, std::vector v, std::vector a, std::vector b);
int construct_roads(std::vector x, std::vector y) {
// Code here...
}
```
由于洛谷技术限制,本题仅包含 IOI 官方数据的部分测试点。
题目描述
在附近的一个公园里,有 $n$ 座**喷泉**,编号为从 $0$ 到 $n - 1$。我们把喷泉看成是二维平面上的点。也就是说,喷泉 $i ~ (0 \leq i \leq n - 1)$ 是一个点 $(x _ i, y _ i)$,这里 $x _ i$ 和 $y _ i$ 是**偶数**。喷泉的位置各不相同。
建筑师 Timothy 受雇来规划一些**道路**的建设,以及每条道路对应的长椅的摆放。每条道路都是一个长度为 $2$ 的**横向**或**纵向**的线段,其端点是两座不同的喷泉。游客应该能够沿着它们即可在任意两座喷泉之间互相抵达。在最开始时,公园里没有任何道路。
对于每条道路,都要在公园里摆放恰好一个长椅,并将其**分配给**(也就是面朝)这条道路。每个长椅必须摆放在某个点 $(a, ~ b)$ 上,这里 $a$ 和 $b$ 都是**奇数**。所有长椅的位置必须都是**不同的**。在 $(a, ~ b)$ 处的长椅,只能分配给两个端点均为 $(a - 1, ~ b - 1), (a - 1, ~ b + 1), (a + 1, ~ b - 1)$ 和 $(a + 1, ~ b + 1)$ 其中之一的道路。举例来说,在 $(3, ~ 3)$ 处的长椅只能分配给下面四条线段所表示的道路之一:$(2, ~ 2), - (2, ~ 4), ~ (2 , ~ 4) - (4, ~ 4), ~ (4, ~ 4) - (4, ~ 2), ~ (4, ~ 2) - (2, ~ 2)$。
请帮助 Timothy 判断一下,能否在满足上述所有要求的前提下,造出所有道路,并摆放和分配长椅。如果这能做到,请给他一个可行的解决方案。如果有多个满足所有要求的方案,你可以报告其中的任意方案。
输入格式
你要实现以下函数:
```cpp
int construct_roads(std::vector x, std::vector y)
```
- $x, ~ y$: 长度为 $n$ 的两个数组。对所有 $i ~ (0 \leq i \leq n - 1)$,喷泉 $i$ 是一个点 $(x[i], y[i]$,这里 $(x[i], y[i])$ 都是偶数。
- 如果存在某个建设方案,函数应当调用 `build`(参见下文)恰好一次来报告建设方案,并紧接着返回 $1$。
- 否则,函数应当返回 $0$,并且不做 `build` 的任何调用。
- 该函数将被调用恰好一次。
你实现的函数可以调用下面的函数,以提供一个可行的道路建设与长椅摆放方案。
```cpp
void build(std::vector u, std::vector v, std::vector a, std::vector b)
```
- 设 $m$ 为建设方案中道路的个数。
- $u, v$: 长度为 $m$ 的两个数组,表示要建设的道路。这些道路的编号为从 $0$ 到 $m - 1$。对所有的 $j ~ (0 \leq j \leq m - 1)$,道路 $j$ 要连接喷泉 $u[j]$ 和 $v[j]$。每条道路必须是长度为 $2$ 的横向或纵向线段。任意两条不同的道路,最多只能有一个公共端点(某个喷泉)。这些道路在建成之后,必须能够沿着它们就可以在任意两个喷泉之间相互抵达。
- $a, b$: 长度为 $m$ 的两个数组,表示长椅。对所有的 $j ~ (0 \leq j \leq m - 1)$,将在 $(a[j], b[j])$ 处摆放一个长椅,并且分配给道路 $j$。不同的长椅不能摆放在同一位置。
输出格式
无
说明/提示
**例 1**
考虑如下调用:
```cpp
construct_roads([4, 4, 6, 4, 2], [4, 6, 4, 2, 4])
```
这意味着总共有 $5$ 座喷泉:
- 喷泉 $0$ 坐落在 $(4, 4)$ 处。
- 喷泉 $1$ 坐落在 $(4, 6)$ 处。
- 喷泉 $2$ 坐落在 $(6, 4)$ 处。
- 喷泉 $3$ 坐落在 $(4, 2)$ 处。
- 喷泉 $4$ 坐落在 $(2, 4)$ 处。
可以建造下面这样 $4$ 条道路,其中每条道路连接两座喷泉,并且摆放着对应的长椅。
| 道路编号 | 道路所连接的喷泉编号 | 所分配的长椅的位置 |
| :----------: | :----------: | :----------: |
| $0$ | $0, 2$ | $(5, 5)$ |
| $1$ | $0, 1$ | $(3, 5)$ |
| $2$ | $3, 0$ | $(5, 3)$ |
| $3$ | $4, 0$ | $(3, 3)$ |
该方案对应下图:
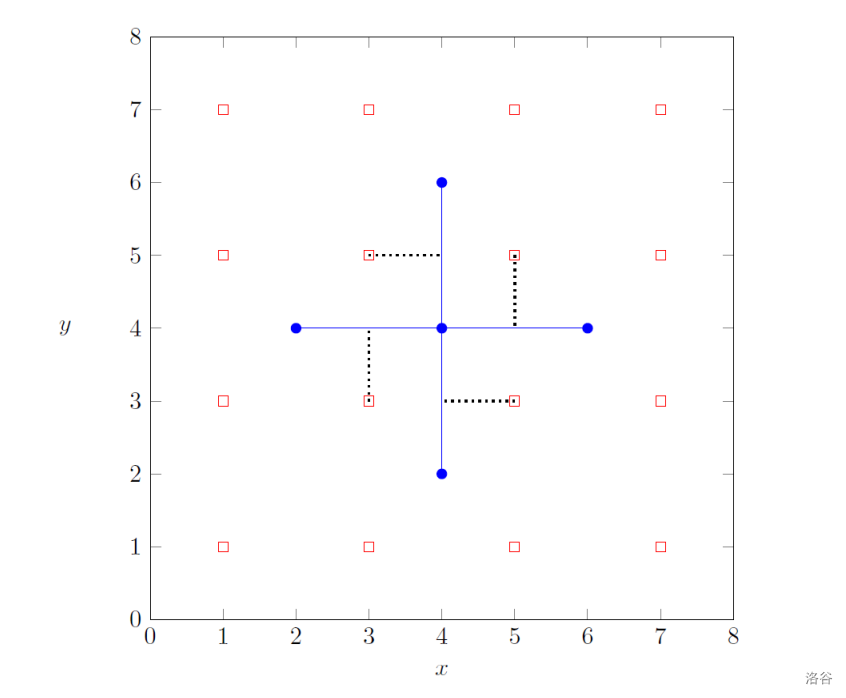
为报告此方案,`construct_roads` 应做如下调用:
```cpp
build([0, 0, 3, 4], [2, 1, 0, 0], [5, 3, 5, 3], [5, 5, 3, 3])
```
随后它应当返回 $1$,
注意,在这个例子中,有多个满足要求的方案,它们都被视为正确。
**例 2**
考虑如下调用:
```cpp
construct_roads([2, 4], [2, 6])
```
喷泉 $0$ 坐落在 $(2, 2)$ 处,而喷泉 $1$ 坐落在 $(4, 6)$ 处。由于不可能建造出满⾜要求的道路,
`construct_roads` 应当返回 $0$,并且不做 `build` 的任何调⽤。
**约束条件**
- $1 \leq n \leq 2 \times 10 ^ 5$
- $2 \leq x[i], y[i] \leq 2 \times 10 ^ 5$
- $x[i], y[i]$ 都是偶数。
- 任意两座喷泉的位置都不相同。
**子任务**
1. ($5$ 分)$x[i] = 2$
2. ($10$ 分)$2 \leq x[i] \leq 4$
3. ($15$ 分)$2 \leq x[i] \leq 6$
4. ($20$ 分)至多只有一种道路建设方案,能够让游客在任意两座喷泉之间沿着这些道路即可抵达。
5. ($20$ 分)任意四座喷泉都不会构成某一个 $2 \times 2$ 正方形的四个顶点。
6. ($30$ 分)没有额外的约束条件。