P8596 「KDOI-02」一个截的拦

## 本题疑似是错题，详情见 [讨论](/discuss/1032942)。 「{!@@(*@@￥';l]dw@)%)%&^_^}（可恶的人类！我一定会回来的！）」 它将飞船拉到了最高速度，试图离开这个充满人类的地狱。 ……

过了那么多年，外星人的飞船速度早已比不过地球的飞船。因此，它决定使用折跃点逃离。 平面地图上有 $n$ 个折跃点，坐标分别为 $(x_i,y_i)$。某些折跃点之间有双向空间隧道连接，共 $m$ 条隧道，每条隧道分别连接折跃点 $u_i,v_i$，且激活该隧道需要消耗 $w_i$ 单位能量。**请注意，为了保证空间隧道之间互不干扰，对于任意两条空间隧道 $\bm{i,j}$，都保证连接点 $\bm{u_i,v_i}$ 与点 $\bm{u_j,v_j}$ 的线段没有交点。保证不存在起点和终点都相同的两条空间隧道。** 外星人的科技非常神奇，因此为了成功折跃离开，外星人必须经过地图上的所有折跃点 **至少一次**，它可以从任意一点开始折跃并从任意一点结束折跃，最终，外星人所花费的总能量为激活路径上所有隧道所消耗能量的 **按位或运算和**。经过两次或两次以上同一隧道只需激活一次该隧道。 外星人的飞船上拥有 $x$ 单位能量，因此，它所选择的折跃方案花费的总能量不能超过 $x$。为了拦截外星人，地方可以执行以下操作任意多次： + 选择一条连接 $u$ 和 $v$ 的双向隧道（你需要保证在点 $u$ 和 $v$ 之间存在双向隧道连接）； + 将激活它所需要的能量增加 $w$（$w\ge0$ 且操作后激活该通道所需要的能量不能超过 $2^{31}-1$）。 其中，$u,v,w$ 都可以自行指定。**每次操作所需要的代价为 $w$ 的二进制表示下 $1$ 的个数。**（即 `c++` 中的 `__builtin_popcount()` 函数） 为了赎罪，你需要设计一种操作方案，使得外星人无法通过折跃逃离，并最小化该方案所需要的代价。

从标准输入读入数据。 输入的第一行包含 $1$ 个正整数 $W$，表示该测试点的评分参数。 输入的第二行包含 $3$ 个整数 $n,m,x$，分别表示折跃点个数，双向隧道条数以及外星人飞船上拥有的能量。 第 $3$ 至 $(n+2)$ 行，第 $(i+2)$ 行有 $2$ 个整数 $x_i,y_i$，表示第 $i$ 个折跃点的坐标。 接下来 $m$ 行，每行 $3$ 个整数 $u_i,v_i,w_i$，表示每条双向隧道连接的两个折跃点和激活所需能量。

输出到标准输出。 **本题采用自定义校验器（special judge）评测。** 输出的第一行应包含一个非负整数 $k$，表示操作总次数。 接下来 $k$ 行，每行一次操作，形如 $u~v~w$，表示将激活连接 $u$ 和 $v$ 的双向隧道所需能量增加 $w$。 你需要保证 $0\le k\le 10000$，否则将被判定为不合法答案。

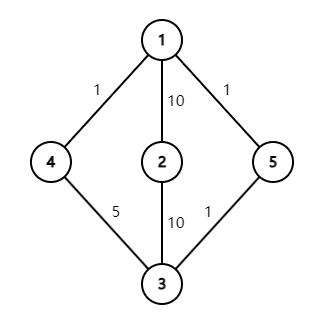
**【样例解释】** + **样例 1 解释：** 经过操作后的平面地图如下图所示（省略坐标轴）：  由于与 $2$ 号折跃点相连的空间隧道所需要的激活能量全部为 $10$，所以成功折跃所需要的能量至少为 $10$，因此外星人无法通过折跃逃离，代价为 $1$，显然不存在代价更小的操作方案。 *** **【评分方式】** 对于每个测试点，如果你的操作方案不合法或使得外星人能够成功通过折跃逃离，你将在该测试点得到 $0$ 分。 否则，设该测试点的评分参数为 $W$，标准答案的代价为 $a$，你的操作方案的代价为 $b$，则你的分数 $s$ 将由下列公式给出： $$ s=\max\left(1-\frac{b-a}{a}\times W,0\right)\times10 $$ *** **【数据范围】** 对于 $100\%$ 的数据，$12\le n\le 53280$，$n-1\le m\le 3n-6$，$0\le x