P8950 [YsOI2022] 道路修建

Ysuperman 正在给他幼儿园里的小朋友们准备一场模板测试，下面是一道模板题，他希望你可以帮他验一下题目。

某地新建了 $n$ 座城市，拟定建造 $m$ 条**单向**道路，其中第 $i$ 条道路起点为 $u_i$，终点为 $v_i$，建造费用为正整数 $w_i$。 然而在道路开始修建之前突发紧急情况，需要马上选择这些道路中的一些来修建使得所有城市的人都可以走到某 $k$ 座城市中（也就是说，所有城市的人都可以走到这 $k$ 座城市中的**至少一座**城市中），你想要知道，如果这 $k$ 座城市是等概率随机在 $n$ 座城市中的选定的，那么期望的最小修建费用是多少。 为了避免分数输入输出，你只需要输出答案对 $998244353$ 取模的结果。

第一行三个非负整数 $n,m,k$ 表示城市数量、拟定建造公路数量以及待选定的城市数量。 接下来 $m$ 行，每行三个正整数 $u_i,v_i,w_i$ 描述一条拟定建造的单向公路。

特别的，如果存在一种选定 $k$ 座城市的方式使得无论如何修建道路都总存在某座城市无法到达这 $k$ 座城市中的任意一座，请输出 `-1`。 否则输出一行一个整数表示答案对 $998244353$ 取模的结果。

#### 样例 1 解释 总共有三种选定集合城市的方案： 1. 选定集合在城市 $1$，那么选择建造 $2\to 1,3\to 1$ 两条道路花费最少，为 $2+4=6$。 2. 选定集合在城市 $2$，那么选择建造 $1\to 2,3\to 1$ 两条道路花费最少，为 $1+4=5$。 3. 选定集合在城市 $3$，那么选择建造 $1\to 2,2\to 3$ 两条道路花费最少，为 $1+3=4$。 所以期望最小花费为 $(6+5+4)/3=5$。 #### 样例 2 解释 有 $6$ 种选择集合城市的方法： 1. 选城市 $1,2$，最小花费 $9$。 2. 选城市 $1,3$，最小花费 $6$。 3. 选城市 $1,4$，最小花费 $7$。 4. 选城市 $2,3$，最小花费 $5$。 5. 选城市 $2,4$，最小花费 $6$。 6. 选城市 $3,4$，最小花费 $3$。 所以期望最小花费为 $(9+6+7+5+6+3)\div 6=6$。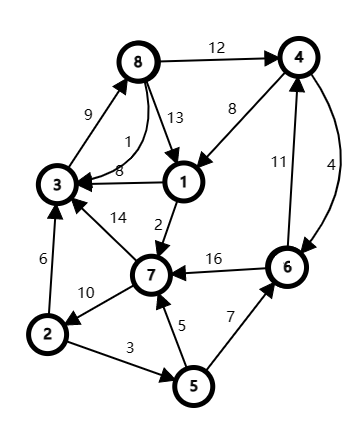 #### 样例 3 解释 这里太小写不下，只配个图算了：  #### 样例 4 解释 当集合城市选在 $1,2,3$ 时，城市 $4$ 无论如何都无法达到 $1,2,3$ 中的任意一个，所以答案为 $-1$。 #### 数据范围 对于 $10\%$ 的数据，满足 $n\le 15$，$m\le 30$。 对于 $30\%$ 的数据，满足 $n\le 20$，$m\le 50$。 另有 $5\%$ 的数据，满足所有 $w_i$ 相等。 另有 $5\%$ 的数据，满足 $k=n$。 另有 $5\%$ 的数据，满足 $k=n-1$。 另有 $10\%$ 的数据，满足 $m=n$。 另有 $20\%$ 的数据，满足 $k=1$。 对于 $100\%$ 的数据，满足 $2\le n\le 10^5$，$1\le m\le 2\times 10^5$，$1\le k\le n$，$1\le u_i,v_i\le n$，$0\le w_i\le 998244352$。