P9000 [CEOI 2022] Measures

有 $N$ 个站在数轴上的人，他们的初始位置分别为 $a_1,a_2,\ldots,a_N$，他们可以以 $1$ 个单位长度每秒的速度移动。 因为众所周知的原因，他们需要保持社交距离，也就是说在任两个人之间距离至少为 $D$。 Alenka 设计了一个 app 来快速求出这 $N$ 个人通过移动来保持社交距离的最小时间，现在她想要添加一个新功能：支持动态加入一个位置为 $b_i$ 的人。 你需要实现一个程序完成这个功能。

第一行三个整数 $N,M,D$。 接下来一行 $N$ 个整数 $a_1,\ldots,a_N$，表示初始的 $N$ 个人。 接下来一行 $M$ 个整数 $b_1,\ldots,b_M$，表示顺次加入的 $M$ 个人。

输出一行 $M$ 个数，第 $i$ 个数表示加入第 $i$ 个人之后所花费的最小时间，你需要输出这个时间的精确值，不含末尾多余的 $0$。

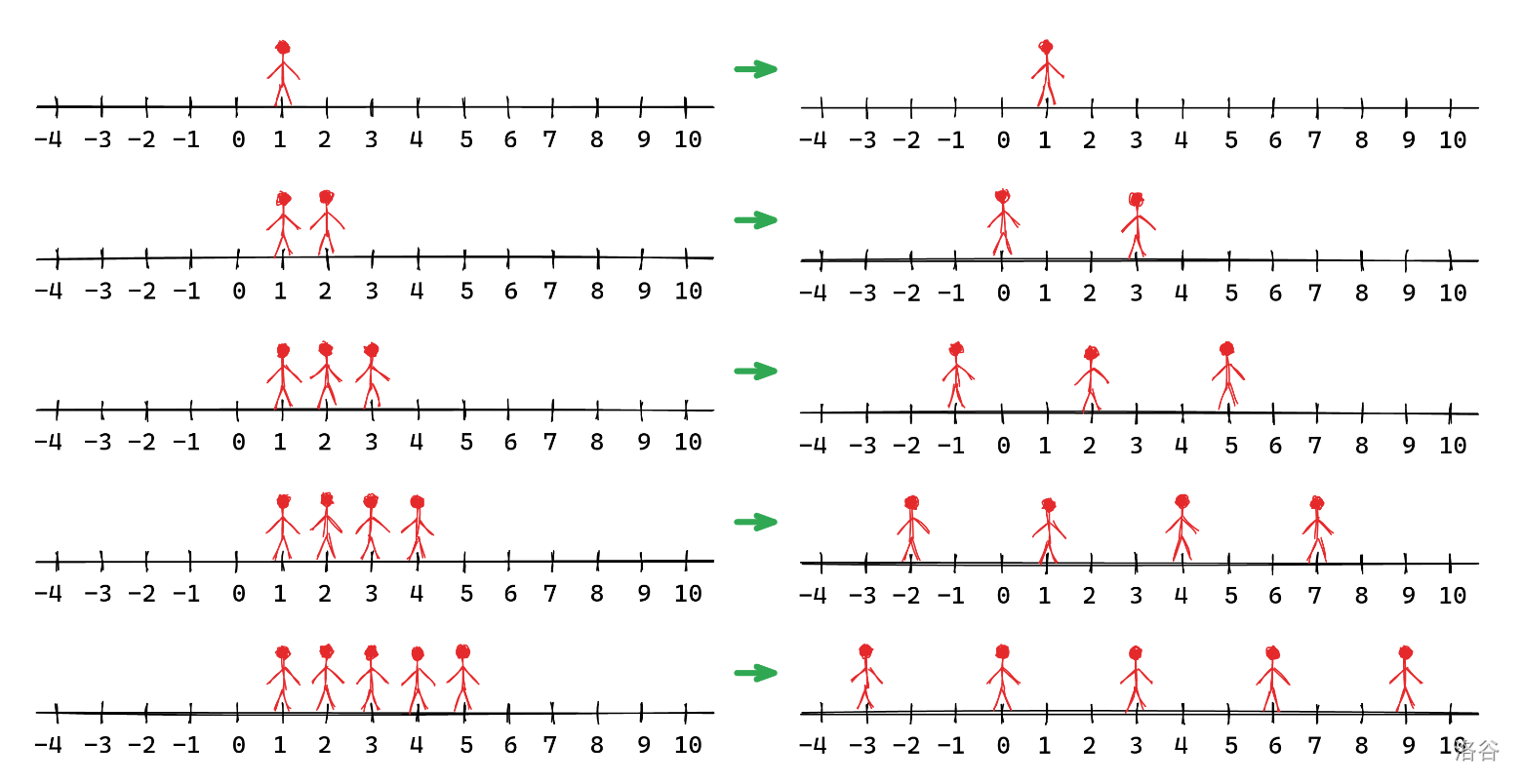
### 样例 2 解释  ### 数据规模与约定 对于全部数据，$1\le D,a_1,\ldots,a_N,b_1,\ldots,b_M\le 10^9$。 | Subtask 编号 | 特殊限制 | 分数 | | :----------: | :-----------------------------------------------------: | :--: | | $1$ | $0\le N\le 2000$，$1\le M\le 10$ | $10$ | | $2$ | $0\le N\le 2\times 10^5$，$1\le M\le 10$ | $14$ | | $3$ | $N=0$，$1\le M\le 2\times 10^5$，$b_1\le \cdots\le b_M$ | $35$ | | $4$ | $N=0$，$1\le M\le 2\times 10^5$ | $41$ |