P9077 [PA 2018] Poddrzewo

**题目译自 [PA 2018](https://sio2.mimuw.edu.pl/c/pa-2018-1/dashboard/) Runda 1 [Poddrzewo](https://sio2.mimuw.edu.pl/c/pa-2018-1/p/pod/)** 给定一个长度为 $n$ 的序列 $a$。 构造一个结点数为 $k$ 的无根树，结点编号分别为 $1 \cdots k$。该树第 $i$ 个结点的度数为 $a_i$。 有可能无解，你可以进行如下操作来使其有解： 1. 修改序列中第 $i$ 个数。 1. 删除序列中第 $i$ 个数。 1. 交换序列中第 $i,j$ 个数。 可以证明，进行有限次操作后一定有解。 你的任务是 **最小化操作 $1$ 使用的次数**。

一行一个整数 $n$，表示序列 $a$ 的长度。 下一行有 $n$ 个整数，第 $i$ 个整数表示 $a_i$。

第一行一个整数 $x$ ，表示操作 $1$ 使用次数最小值。 第二行一个整数 $k\ (2 \le k \le n)$，表示你构造的树结点数目。 接下来 $k-1$ 行，每行两个数 $u,v\ (1 \le u, v \le k)$，表示连接第 $u,v$ 个结点。 多解输出任意解。

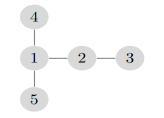
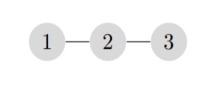
#### 样例 1 解释 我们可以删除第 $3$ 个数字，然后更改元素的顺序。 得到最后的序列为 $(3,2,1,1,1)$。 这是构造的树的示意图：  ------------ #### 样例 2 解释 我们可以修改第 $3$ 个数字，得到最后的序列为 $(1,2,1)$。可以证明，操作 $1$ 至少需要使用 $1$ 次。 这是构造的树的示意图：  ------------ #### 数据范围 **本题采用捆绑测试** 对于 $100\%$ 的数据： - $2 \le n \le 10^6$ - $1 \le a_i \le n-1$ 保证存在至少一个子任务，其中操作 $1$ 使用次数最小值为 $0$。