P9079 [PA 2018] Heros
题目描述
**题目译自 [PA 2018](https://sio2.mimuw.edu.pl/c/pa-2018-1/dashboard/) Runda 2 [Heros](https://sio2.mimuw.edu.pl/c/pa-2018-1/p/her/)**
给定一个有向无环图,该图有 $n$ 个节点, $m$ 条有向边。
你需要从中删除 $k$ 个点以及与其关联的边,使得图中的最长链最短。
输入格式
第一行三个整数,分别表示 $n$ , $m$ , $k$。
接下来 $m$ 行,每行两个整数 $x$ , $y$ ,表示从 $x$ 点到 $y$ 点有一条有向边。
输出格式
一行一个整数,表示图中最长链的长度最小值。
说明/提示
#### 样例 1 解释
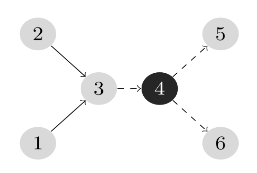
删除编号为 $4$ 的点后,图中的最长链长度为 $2$ 。即为我们可以得到的最长链长度的最小值。可以验证所有方案中图中最长链长度最小为 $2$ 。
------------
#### 数据范围
**本题采用捆绑测试**
对于 $100\%$ 的数据:
- $1 \le n \le 300$
- $0 \le m \le 400$
- $0 \le k \le \min(n,4)$
- $1 \le x < y \le n$