P9085 [PA 2018] Wielokąty

**题目译自 [PA 2018](https://sio2.mimuw.edu.pl/c/pa-2018-1/dashboard/) Runda 5 [Wielokąty](https://sio2.mimuw.edu.pl/c/pa-2018-1/p/wie/)** 。 请求出满足以下条件的多边形的个数： - 记该多边形的第 $i$ 个顶点为$(x_i,y_i)$ ，则 $x_i,y_i \in \mathbb{Z}$ 且 $1 \le x_i \le X$ , $1 \le y_i \le Y$ 。 - 该多边形的任意一条边（不包含端点）不能经过格点（即横纵坐标都为整数的点）。 - 该多边形的每一条边的长度都是不超过 $K$ 的整数。 - 该多边形是一个凸多边形，而且不能退化（不能出现三点共线，自切，不小于 $180 ^{\circ}$ 的角）。 - 该多边形的每一条边都是线段。 由于满足条件的多边形数量太大，你只需要输出其对 $2^{32}$ 取模后的值即可。 下图展示了三个不合法的多边形。第一个多边形的边经过了格点，第二个多边形退化了，第三个多边形不是凸的。而且第一，三个有的边长不是整数。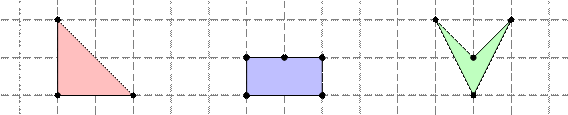  我们将两个多边形看做不相同的多边形，当且仅当它们有至少一个顶点不相同。

输入只有一行，包含三个正整数 $X,Y,K$。

输出一行一个整数，即为满足条件的多边形的数量对 $2^{32}$ 取模后的值。

#### 样例 1 解释 下图展示了 $42$ 个合法多边形中的一个多边形。 可以验证，该多边形满足每一个条件。  ------------ #### 数据范围 **本题采用捆绑测试** 对于 $100\%$ 的数据，保证 $1 \le X,Y \le 10^9,1 \le K \le 250$ 。