[春季测试 2023] 涂色游戏

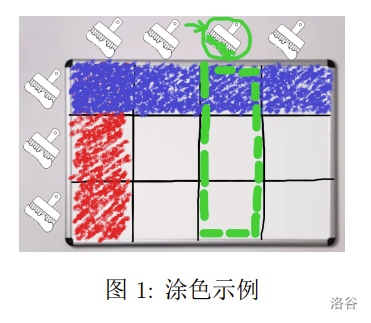
有一天，小 D 在刷朋友圈时看到了一段游戏视频。 这个游戏的名字叫涂色游戏，视频中的游戏界面是一个 $n$ 行 $m$ 列的网格，初始时每一个格子都是白色（用数字 $0$ 表示）。其中每一行的左侧、每一列的上方都有一把带颜色的刷子。玩家点击某个刷子后，这个刷子会将其右侧（或下方）的一整行（或一整列）涂上同一种颜色，**该行（或该列）格子原有的颜色都会被覆盖成新涂上的颜色。** 下图展示的情况可以通过先将第一列涂成红色，然后将第一行涂成蓝色得到，若此时选择将第三列涂成绿色，则图中绿色方框中的格子都会变成绿色。  小 D 想用他自己编写的程序来进行视频中的游戏。在编程的过程中，小 D 在涂色逻辑的实现上却遇到了一些困难，于是他向你求助，希望你能帮他完成实现涂色逻辑部分的代码。 首先，小 D 会给你网格的行数和列数 $n, m$，然后给出 $q$ 次操作，每次操作用三个整数 $opt_i, x_i, c_i$ 表示： - 如果 $opt_i=0$，那么这次操作会将第 $x_i$ **行**涂成颜色 $c_i$。 - 如果 $opt_i=1$，那么这次操作会将第 $x_i$ **列**涂成颜色 $c_i$。 在所有涂色操作结束以后，你需要输出网格中每个位置的颜色是什么。

**本题有多组测试数据。** 第一行包含一个正整数 $T$，表示数据组数。 接下来一共 $T$ 组数据，每组数据格式如下： 第一行包含三个整数 $n, m, q$，分别表示涂色板的行数、列数，以及小 D 进行涂色操作的次数。 接下来 $q$ 行，每行包含三个整数 $opt_i, x_i, c_i$，表示一次操作。

对于每组数据，输出 $n$ 行，每行 $m$ 个由单个空格隔开的整数。 其中第 $i$ 行第 $j$ 个整数表示涂色完成后网格中第 $i$ 行第 $j$ 列的方格是什么颜色。

2
5 5 9
1 5 1
0 4 0
1 4 1
0 3 0
1 3 1
0 2 0
1 2 1
0 1 0
1 1 1
3 3 3
0 1 2
0 3 1
1 1 3

1 0 0 0 0
1 1 0 0 0
1 1 1 0 0
1 1 1 1 0
1 1 1 1 1
3 2 2
3 0 0
3 1 1

**【样例 1 解释】** 注意当一个格子没有被涂色时，其颜色为白色，用数字 $0$ 表示。 **【样例 2】** 见选手目录下的 paint/paint2.in 与 paint/paint2.ans。 **【数据范围】** 对于所有数据，保证： - $1 \leq T \leq 10$，$1 \leq n,m \leq 10^5$，$0 \leq q \leq 10^5$，$0 \leq c_i \leq 10^9$。 - 若 $opt_i=0$，则 $1 \leq x_i \leq n$；若 $opt_i=1$，则 $1 \leq x_i \leq m$。 - 单个测试点中所有数据的 $n \cdot m$ 的总和不超过 $10^6$，$q$ 的总和不超过 $10^6$。 |测试点|$n \le$|$m \le$|$q \le$|性质 A|性质 B| |:-:|:-:|:-:|:-:|:-:|:-:| |1|$1$|$1$|$0$|√|√| |2|$1$|$1$|$1$|√|√| |3|$1$|$10$|$20$|√|√| |4|$1$|$10^5$|$10^5$|×|√| |5|$1$|$10^5$|$10^5$|×|√| |6|$1$|$10^5$|$10^5$|×|×| |7|$10$|$10$|$20$|√|√| |8|$50$|$50$|$100$|√|√| |9|$50$|$50$|$100$|√|×| |10|$1000$|$1000$|$2000$|×|√| |11|$1000$|$1000$|$2000$|×|×| |12|$1000$|$1000$|$2000$|×|×| |13|$1000$|$1000$|$10^5$|×|×| |14|$1000$|$1000$|$10^5$|×|×| |15|$10^5$|$10^5$|$10^5$|√|√| |16|$10^5$|$10^5$|$10^5$|√|√| |17|$10^5$|$10^5$|$10^5$|√|×| |18|$10^5$|$10^5$|$10^5$|√|×| |19|$10^5$|$10^5$|$10^5$|×|×| |20|$10^5$|$10^5$|$10^5$|×|×| 特殊性质 A：保证测试点中所有的 $q \cdot \max(n, m)$ 之和不超过 $10^7$。 特殊性质 B：保证 $opt_i = 1$。 **【提示】** 数据千万条，清空第一条。多测不清空，爆零两行泪。