P9209 Undying "Phoenix Tail"

Phoenix Tail is a mass-produced feather. It can be used as medicine. Even though it is mass-produced, where can we get this all-purpose medicine?

There is a parking lot with $n$ parking spaces arranged in a single line, with walls on both the far left and far right. There are $n$ cars that will park in this lot in order. When parking the $i$-th car, the more empty spaces there are on the left and right of the chosen spot, the less time it takes to park. Specifically, if the number of consecutive empty spaces on its left is $l$ and on its right is $r$, then the time needed to park this car is $W_i-L_i\cdot l-R_i\cdot r$, where $W_i, L_i, R_i$ are given. (In particular, the parking time will not be negative, so we guarantee $W_i\ge L_i\cdot n+R_i\cdot n$.) Explanation of consecutive empty spaces: for example, in the figure below, the position pointed to by the arrow has $1$ consecutive empty space on the left and $2$ consecutive empty spaces on the right.  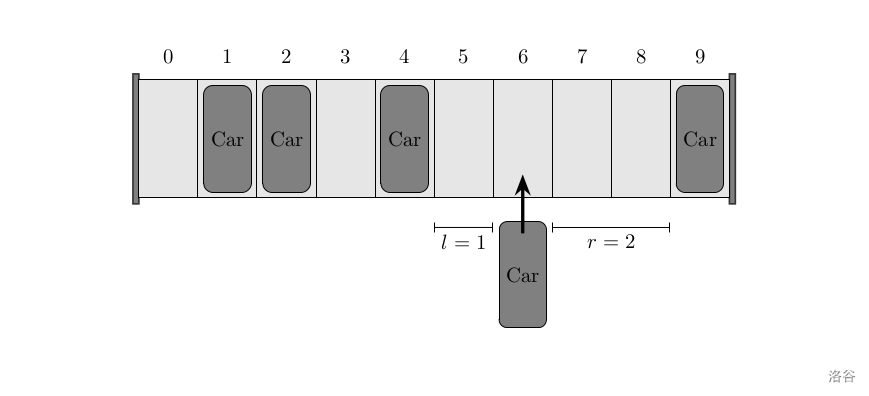Please determine the parking position for each car in order, so that the total time to park all cars is minimized.

The first line contains an integer $n$. The next three lines each contain $n$ integers. In the first of these lines, the $i$-th number gives $W_i$; in the second line, the $i$-th number gives $L_i$; in the third line, the $i$-th number gives $R_i$. It is guaranteed that $W_i\ge L_i\cdot n+R_i\cdot n$ and $L_i,R_i\ge 0$.

Output one number, the minimum total time required.

#### Sample Explanation 1 The first car parks in the $3$-rd parking space from left to right. At this time, there are $2$ consecutive empty spaces on the left of this space and no consecutive empty spaces on the right, so the time needed is $18-1\times 2-1\times 0=16$. The second car parks in the $1$-st parking space from left to right. At this time, there are no consecutive empty spaces on the left and $1$ consecutive empty space on the right, so the time needed is $20-2\times 0-4\times 1=16$. The third car parks in the $2$-nd parking space from left to right. At this time, there are no consecutive empty spaces on either side, so the time needed is $22-3\times 0-3\times 0=22$. The total time to park all cars is $16+16+22=54$. #### Constraints For all testdata, it is guaranteed that $1\le n\le 10^5$, $0\le L_i,R_i\le 10^5$, and $nL_i+nR_i\le W_i\le 2\times 10^{10}$. Translated by ChatGPT 5